题目内容
等差数列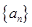 中,
中,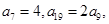
(I)求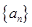 的通项公式;
的通项公式;
(II)设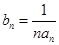 ,求数列
,求数列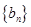 的前n项和
的前n项和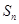 .
.
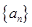 中,
中,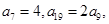
(I)求
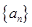 的通项公式;
的通项公式;(II)设
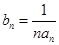 ,求数列
,求数列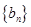 的前n项和
的前n项和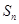 .
.(I) (II)
(II)
 (II)
(II)
(Ⅰ)设等差数列 的公差为d,则
的公差为d,则
因为 ,所以
,所以 .
.
解得 .
.
所以 的通项公式为
的通项公式为 .
.
(Ⅱ) ,
,
所以 .
.
(1)利用基本量思想求解,通过解方程求解等差数列的首项和公差;(2)利用裂项相消法求解;数列求和,作为高考大题中的一个模块,需要同学们掌握好最基本的几种数列求和的方法以及何时使用:①基本公式法:题设中告知是等差数列或者等比数列;②裂项相消法:分式型或根式型;③错位相减法:等差×等比;④分组求和法:等差+等比;⑤错位相减法:首尾相加产生某些规律.
【考点定位】等差数列通项公式和数列求和
 的公差为d,则
的公差为d,则
因为
 ,所以
,所以 .
.解得
 .
.所以
 的通项公式为
的通项公式为 .
.(Ⅱ)
 ,
,所以
 .
.(1)利用基本量思想求解,通过解方程求解等差数列的首项和公差;(2)利用裂项相消法求解;数列求和,作为高考大题中的一个模块,需要同学们掌握好最基本的几种数列求和的方法以及何时使用:①基本公式法:题设中告知是等差数列或者等比数列;②裂项相消法:分式型或根式型;③错位相减法:等差×等比;④分组求和法:等差+等比;⑤错位相减法:首尾相加产生某些规律.
【考点定位】等差数列通项公式和数列求和

练习册系列答案
相关题目
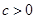 ,定义函数
,定义函数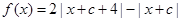 ,数列
,数列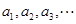 满足
满足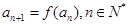 .
.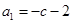 ,求
,求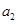 及
及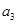 ;
;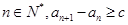 ,;
,;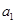 ,使得
,使得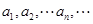 成等差数列?若存在,求出所有这样的
成等差数列?若存在,求出所有这样的 的前
的前 项和为
项和为 ,若
,若 ,则
,则 。
。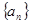 的前
的前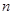 项和为
项和为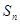 ,且
,且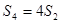 ,
,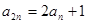 .
.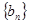 满足
满足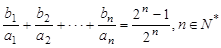 ,求
,求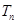 .
.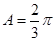 =1,d=3确定的等差数列
=1,d=3确定的等差数列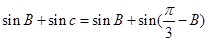 ,当
,当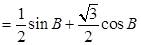 =298是,n等于
=298是,n等于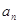 )满足
)满足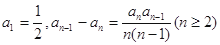 ,则该数列的通项公式
,则该数列的通项公式 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足 .令
.令
 ,记数列
,记数列 的前
的前 项和为
项和为 ,对任意的
,对任意的 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的最小值是 .
的最小值是 . 的公差为2,若
的公差为2,若 成等比数列,则
成等比数列,则 =( )
=( )



 中,
中, ,
, ,则
,则 ______;设
______;设 ,则数列
,则数列 的前
的前 项和
项和 ______.
______.