题目内容
给定常数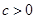 ,定义函数
,定义函数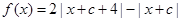 ,数列
,数列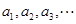 满足
满足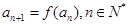 .
.
(1)若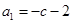 ,求
,求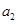 及
及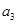 ;
;
(2)求证:对任意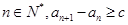 ,;
,;
(3)是否存在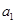 ,使得
,使得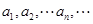 成等差数列?若存在,求出所有这样的
成等差数列?若存在,求出所有这样的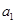 ,若不存在,说明理由.
,若不存在,说明理由.
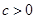 ,定义函数
,定义函数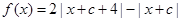 ,数列
,数列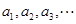 满足
满足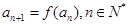 .
.(1)若
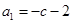 ,求
,求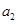 及
及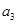 ;
;(2)求证:对任意
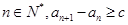 ,;
,;(3)是否存在
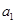 ,使得
,使得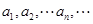 成等差数列?若存在,求出所有这样的
成等差数列?若存在,求出所有这样的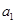 ,若不存在,说明理由.
,若不存在,说明理由.见解析
(1)因为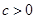 ,
, ,故
,故 ,
,

(2)要证明原命题,只需证明 对任意
对任意 都成立,
都成立,

即只需证明
若 ,显然有
,显然有 成立;
成立;
若 ,则
,则 显然成立
显然成立
综上, 恒成立,即对任意的
恒成立,即对任意的 ,
,
(3)由(2)知,若 为等差数列,则公差
为等差数列,则公差 ,故n无限增大时,总有
,故n无限增大时,总有
此时,
即
故 ,
,
即 ,
,
当 时,等式成立,且
时,等式成立,且 时,
时, ,此时
,此时 为等差数列,满足题意;
为等差数列,满足题意;
若 ,则
,则 ,
,
此时, 也满足题意;
也满足题意;
综上,满足题意的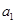 的取值范围是
的取值范围是 .
.
【考点定位】考查数列与函数的综合应用,属难题。
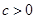 ,
, ,故
,故 ,
,
(2)要证明原命题,只需证明
 对任意
对任意 都成立,
都成立,
即只需证明

若
 ,显然有
,显然有 成立;
成立;若
 ,则
,则 显然成立
显然成立综上,
 恒成立,即对任意的
恒成立,即对任意的 ,
,
(3)由(2)知,若
 为等差数列,则公差
为等差数列,则公差 ,故n无限增大时,总有
,故n无限增大时,总有
此时,

即

故
 ,
,即
 ,
,当
 时,等式成立,且
时,等式成立,且 时,
时, ,此时
,此时 为等差数列,满足题意;
为等差数列,满足题意;若
 ,则
,则 ,
,此时,
 也满足题意;
也满足题意;综上,满足题意的
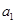 的取值范围是
的取值范围是 .
.【考点定位】考查数列与函数的综合应用,属难题。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 满足
满足 ,则当
,则当 取最小值时
取最小值时 的值为( )
的值为( ) 或
或
 或
或 满足
满足 ,且
,且 .
. 
 ,且{
,且{ }为等差数列?若存在,求出t的值;若不存在,说明理由.
}为等差数列?若存在,求出t的值;若不存在,说明理由.  满足:
满足:
 的前20项的和;
的前20项的和;  满足:
满足: ,求数列
,求数列 项和.
项和. 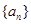 满足
满足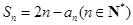 .
.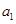 ,
,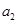 ,
,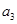 ,
,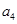 ,由此猜想通项公式
,由此猜想通项公式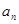 ,并用数学归纳法证明此猜想;
,并用数学归纳法证明此猜想;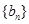 满足
满足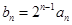 ,求证:
,求证: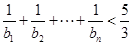 .
.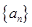 中,
中,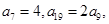
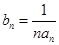 ,求数列
,求数列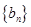 的前n项和
的前n项和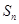 .
.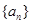 :
: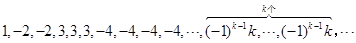 ,即当
,即当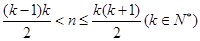 时,记
时,记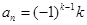 .记
.记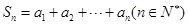 . 对于
. 对于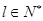 ,定义集合
,定义集合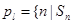 是
是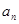 的整数倍,
的整数倍,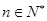 ,且
,且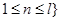 .
.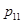 中元素的个数;
中元素的个数;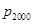 中元素的个数.
中元素的个数. 中,
中, ,且
,且 ,则
,则 .
. 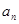 }的前n项和
}的前n项和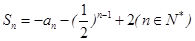 ,数列{
,数列{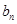 }满足
}满足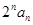 .
.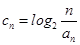 ,数列{
,数列{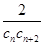 }的前n项和为Tn,求满足
}的前n项和为Tn,求满足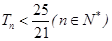 的n的最大值.
的n的最大值.