题目内容
9.设数列{an}的前n项和为Sn,且λSn=λ-an,其中λ≠0且λ≠-1.(1)证明:{an}是等比数列,并求其通项公式;
(2)若${S_4}=\frac{15}{16}$,求λ.
分析 (1)利用已知条件求出数列的首项以及数列相邻两项的关系,利用数列是等比数列,求出公比,然后求解通项公式.
(2)利用数列的通项公式以及已知条件推出λ的关系式,求解即可.
解答 解:(1)当n=1时,λa1=λ-a1,
∵λ≠0且λ≠-1,∴${a_1}=\frac{λ}{1+λ}$,
当n≥2时,λSn-1=λ-an-1,λSn=λ-an,
两式相减得(1+λ)an=an-1,因为λ≠-1,
∴$\frac{a_n}{{{a_{n-1}}}}=\frac{1}{{({1+λ})}}$,
因此{an}是首项为${a_1}=\frac{λ}{1+λ}$,公比为$\frac{1}{{({1+λ})}}$的等比数列,
∴${a_n}=\frac{λ}{1+λ}{({\frac{λ}{1+λ}})^{n-1}}=\frac{λ}{{{{({1+λ})}^n}}}$.
(2)由λSn=λ-an得${S_4}=1-\frac{1}{λ}{a_4}$=$1-\frac{1}{{{{({λ+1})}^4}}}$
∴$1-\frac{1}{{{{({λ+1})}^4}}}=\frac{15}{16}$,
∴λ=1或λ=-3.
点评 本题考查数列的递推关系式的应用,等比数列的通项公式的求法,考查转化思想以及计算能力.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
4.设数列{an}的前n项和为Sn,已知a2=2,an+2+(-1)n-1an=1,则S40=( )
| A. | 260 | B. | 250 | C. | 240 | D. | 230 |
19.在高三一次数学测验后,某班对选做题的选题情况进行了统计,如表.
(Ⅰ)求全班选做题的均分;
(Ⅱ)据此判断是否有90%的把握认为选做《坐标系与参数方程》或《不等式选讲》与性别有关?
(Ⅲ)已知学习委员甲(女)和数学科代表乙(男)都选做《不等式选讲》.若在《不等式选讲》中按性别分层抽样抽取3人,记甲乙两人被选中的人数为,求的数学期望.
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,n=a+b+c+d.
下面临界值表仅供参考:
| 坐标系与参数方程 | 不等式选讲 | |||
| 人数及均分 | 人数 | 均分 | 人数 | 均分 |
| 男同学 | 14 | 8 | 6 | 7 |
| 女同学 | 8 | 6.5 | 12 | 5.5 |
(Ⅱ)据此判断是否有90%的把握认为选做《坐标系与参数方程》或《不等式选讲》与性别有关?
(Ⅲ)已知学习委员甲(女)和数学科代表乙(男)都选做《不等式选讲》.若在《不等式选讲》中按性别分层抽样抽取3人,记甲乙两人被选中的人数为,求的数学期望.
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,n=a+b+c+d.
下面临界值表仅供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
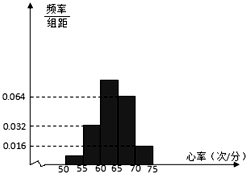 某高校要了解在校学生的身体健康状况,随机抽取了50名学生进行心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60)…第五组[70,75],按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
某高校要了解在校学生的身体健康状况,随机抽取了50名学生进行心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60)…第五组[70,75],按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.