题目内容
2.已知函数f(x)=alnx-x+$\frac{1}{x}$,g(x)=x2+x-b.y=f(x)图象恒过定点P,且P点既在y=g(x)图象上,又在y=f(x)的导函数的图象上.(Ⅰ)求a、b的值;
(Ⅱ)设h(x)=$\frac{f(x)}{g(x)}$,求证:当x>0且x≠1时,h(x)<0.
分析 (1)当x=1时,f(1)=0,所以P(1,0),分别代入f′(x),g(x)求得a,b;
(2)由(1)可得f(x)与g(x)的解析式,对f(x)求导,进而分x∈(0,1)时,x∈(1,+∞)时,分别讨论f(x),g(x)的正负,得出h(x)<0.
解答 解:(1)根据题意,函数f(x)=alnx-x+$\frac{1}{x}$,恒过定点(1,0),
故P的坐标为(1,0),则有g(1)=1+1-b=0,即b=2;
对于f(x)=alnx-x+$\frac{1}{x}$,其导数f′(x)=$\frac{a}{x}$-1-$\frac{1}{{x}^{2}}$,
又由p(1,0),即f′(1)=0,
解可得a=2;
(2)由(1)可得f(x)=2lnx-x+$\frac{1}{x}$,则f′(x)=$\frac{2}{x}$-1-$\frac{1}{{x}^{2}}$=-$\frac{(x-1)^{2}}{{x}^{2}}$,
g(x)=x2+x-2,
当x∈(0,1)时,f′(x)<0,f(x)在(0,1)上单调递减,f(x)>f(1)=0,
易知g(x)<0,故h(x)<0.
当x∈(1,+∞)时,f′(x)<0,f(x)在(0,1)上单调递减,f(x)<f(1)=0,
易知g(x)>0,故h(x)<0.
综上所述,当x>0且x≠1时,h(x)<0.
点评 本题考查单调性与导数故选的应用,函数与不等式的综合,分类讨论的思想和能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.方程x2+y2+Dx+Ey+F=0表示以(-2,3)为圆心,4为半径的圆,则D,E,F的值分别为( )
| A. | 4,-6,3 | B. | -4,6,3 | C. | -4,-6,3 | D. | 4,-6,-3 |
10.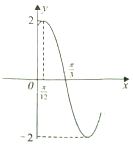 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间是( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间是( )| A. | $[{kπ-\frac{5π}{12},kπ+\frac{π}{12}}],k∈z$ | B. | $[{kπ-\frac{π}{6},kπ+\frac{π}{3}}],k∈z$ | ||
| C. | $[{kπ-\frac{π}{12},kπ+\frac{5π}{12}}],k∈z$ | D. | $[{kπ+\frac{π}{6},kπ+\frac{5π}{6}}],k∈z$ |
7.直线y=-x-1的倾斜角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
