题目内容
13.已知$f(α)=\frac{{sin({\frac{π}{2}-α})sin({-α})tan({π-α})}}{{tan({-α})sin({π-α})}}$.(Ⅰ)化简f(α);
(Ⅱ)若α为第四象限角,且$cos({\frac{3}{2}π-α})=\frac{2}{3}$,求f(α)的值.
分析 (Ⅰ)利用诱导公式化解即可得f(α);
(Ⅱ)根据同角三角函数关系式,可求f(α)的值.
解答 解:(Ⅰ)$f(α)=\frac{{sin({\frac{π}{2}-α})sin({-α})tan({π-α})}}{{tan({-α})sin({π-α})}}$=$\frac{{cosα({-sinα})({-tanα})}}{{({-tanα})sinα}}=-cosα$.
(Ⅱ)由$cos({\frac{3}{2}π-α})=\frac{2}{3}$,得$sinα=-\frac{2}{3}$.
又∵α为第四象限角,
∴$cosα=\sqrt{1-{{sin}^2}α}=\frac{{\sqrt{5}}}{3}$.
故得$f(α)=-\frac{{\sqrt{5}}}{3}$.
点评 本题考查了诱导公式的化简能力和同角三角函数关系式的运用,属于基础题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
18.已知函数f(x)=$\frac{1}{2}$ax2+bx+1,其中a∈{2,4},b∈{1,3},从f(x)中随机抽取1个,则它在(-∞,-1]上是减函数的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{6}$ | D. | 0 |
5.已知函数$f(x)=\frac{lnx}{x+a}({a∈R})$.
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直,求a的值;
(2)讨论方程f(x)=1的实根的情况.
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直,求a的值;
(2)讨论方程f(x)=1的实根的情况.
1.对任意的x,y∈(0,+∞),不等式ex+y-4+ex-y+4+6≥4xlna恒成立,则正实数a的最大值是( )
| A. | $\sqrt{e}$ | B. | $\frac{1}{2}e$ | C. | e | D. | 2e |
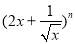 的展开式前两项的二项式系数之和为10.
的展开式前两项的二项式系数之和为10.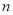 的值.
的值.