题目内容
5.若钝角三角形ABC的三个内角满足:∠A<∠B<∠C,2∠B=∠A+∠C,且最大边长与最小边长的比值为m,则m的取值范围是(2,+∞).分析 由题意可得B=60°,A+C=120°,由正弦定理结合题意可得 m=$\frac{c}{a}=\frac{sinC}{sinA}$=$\frac{\sqrt{3}}{2}$cotA+$\frac{1}{2}$,由于钝角三角形中,C大于90° 可得0<A<30°,利用余切函数的单调性可得答案.
解答 解:在△ABC中,∵∠A<∠B<∠C,2∠B=∠A+∠C,
∴B=60°,A+C=120°.
由正弦定理可得:$\frac{a}{sinA}=\frac{c}{sinC}$,
根据题意可得:m=$\frac{c}{a}=\frac{sinC}{sinA}$.
由于钝角三角形中,C大于90°,
可得:0°<A<30°,
解得:m=$\frac{c}{a}=\frac{sinC}{sinA}$=$\frac{sin(120°-A)}{sinA}$=$\frac{\sqrt{3}}{2}$cotA+$\frac{1}{2}$,
由于$\sqrt{3}$<cotA<+∞,
∴m>2,即m的取值范围是:(2,+∞).
故答案为:(2,+∞).
点评 本题考查正弦定理的应用,大角对大边,正弦函数的值域,化m=$\frac{c}{a}=\frac{sinC}{sinA}$=$\frac{sin(120°-A)}{sinA}$=$\frac{\sqrt{3}}{2}$cotA+$\frac{1}{2}$,是解题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
15.已知函数f(x)的定义域为R,当x>0时,f(x)=log2x,若g(x)=xf(x)为偶函数,则f(-$\frac{1}{2}$)=( )
| A. | 0 | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |

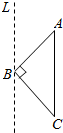 如图,等腰直角三角形ABC,|AB|=$\sqrt{2}$,AC∥L,三角形ABC绕直线L旋转一周,得到的几何体的体积为$\frac{4π}{3}$.
如图,等腰直角三角形ABC,|AB|=$\sqrt{2}$,AC∥L,三角形ABC绕直线L旋转一周,得到的几何体的体积为$\frac{4π}{3}$.