题目内容
已知数列{an}的前n项和Sn=n2+1(n∈N*)
(1)求数列{an}的通项公式;
(2)设cn=
,求数列{cn}的前n项和Tn;
(3)讨论(2)中Tn的最值.
(1)求数列{an}的通项公式;
(2)设cn=
| 1 |
| an•an+1 |
(3)讨论(2)中Tn的最值.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用公式an=
可求出数列{an}的通项an.
(2)n≥2时,cn=
=
=
(
-
),利用裂项相消法求和;
(3)利用(2)的结论,即可得出Tn的最值.
|
(2)n≥2时,cn=
| 1 |
| an•an+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
(3)利用(2)的结论,即可得出Tn的最值.
解答:
解:(1)∵Sn=n2+1
∴a1=S1=1+1=2,
∴当n≥2时,an=Sn-Sn-1=(n2+1)-[(n-1)2+1]=2n-1,
当n=1时,2n-1=1≠a1,
∴an=
.
(2)n≥2时,cn=
=
=
(
-
),
∴当n=1时,Tn=c1=
=
=
,
当n≥2时,Tn=c1+c2+…+cn=
+
(
-
+
-
+…+
-
)=
+
(
-
)=
-
,
∴Tn=
.
(3)由(2)Tn的最小值为
,无最大值.
∴a1=S1=1+1=2,
∴当n≥2时,an=Sn-Sn-1=(n2+1)-[(n-1)2+1]=2n-1,
当n=1时,2n-1=1≠a1,
∴an=
|
(2)n≥2时,cn=
| 1 |
| an•an+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴当n=1时,Tn=c1=
| 1 |
| a1a2 |
| 1 |
| 2×3 |
| 1 |
| 6 |
当n≥2时,Tn=c1+c2+…+cn=
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n+1 |
| 1 |
| 3 |
| 1 |
| 4n+2 |
∴Tn=
|
(3)由(2)Tn的最小值为
| 1 |
| 6 |
点评:本题考查数列的性质和应用,考查利用公式法求数列的通项公式及利用裂项相消法求数列的和知识,解题时要注意公式的灵活运用.

练习册系列答案
相关题目
下列椭圆的形状哪一个更圆( )
| A、9x2+y2=36 | ||||
B、
| ||||
| C、x2+9y2=36 | ||||
D、
|
已知椭圆
+
=1(a>b>0),过焦点F1的弦AB的长是2,另一焦点为F2,则△ABF2的周长是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2a | B、4a-2 |
| C、4a | D、4a+4 |
圆心角为1rad,半径为1的扇形的面积为( )
| A、1 | ||
B、
| ||
C、
| ||
| D、π |
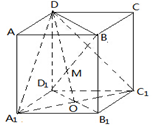 如图,正方体ABCD-A1B1C1D1中,对角线BD1与过A1、D、C1的平面交于点M,则
如图,正方体ABCD-A1B1C1D1中,对角线BD1与过A1、D、C1的平面交于点M,则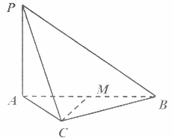 如图,三棱锥P-ABC中,PA⊥底面ABC,△ABC是正三角形,AB=4,PA=3,M是AB的中点.
如图,三棱锥P-ABC中,PA⊥底面ABC,△ABC是正三角形,AB=4,PA=3,M是AB的中点.