题目内容
函数f(x)的导函数为f′(x),若对于定义域内任意x1、x2(x1≠x2),有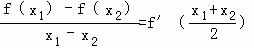 恒成立,则称f(x)为恒均变函数.给出下列函数:
恒成立,则称f(x)为恒均变函数.给出下列函数:
①f(x)=2x+3;②f(x)=x2﹣2x+3;③f(x)=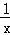 ;④f(x)=ex;⑤f(x)=lnx.
;④f(x)=ex;⑤f(x)=lnx.
其中为恒均变函数的序号是 .(写出所有满足条件的函数的序号)
解:对于①f(x)=2x+3, =
= =2,
=2, =2,满足
=2,满足 ,为恒均变函数.对于②f(x)=x2﹣2x+3,
,为恒均变函数.对于②f(x)=x2﹣2x+3, =
= =
= =x1+x2﹣2
=x1+x2﹣2
 =2•
=2• ﹣2=x1+x2﹣2,故满足
﹣2=x1+x2﹣2,故满足 ,为恒均变函数.
,为恒均变函数.
对于;③ ,
, =
= =
= ,
, =﹣
=﹣ =
= ,显然不满足
,显然不满足 ,故不是恒均变函数.
,故不是恒均变函数.
对于④f(x)=ex , =
= ,
, =
= ,显然不满足
,显然不满足
 ,故不是恒均变函数.对于⑤f(x)=lnx,
,故不是恒均变函数.对于⑤f(x)=lnx, =
= =
= ,
, =
= ,显然不满足
,显然不满足  ,故不是恒均变函数.故答案为 ①②.
,故不是恒均变函数.故答案为 ①②.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 ,则“
,则“ ”是“
”是“
 ,
, 的解集
的解集 .求
.求
 的值;
的值; 求
求 的最小值.
的最小值. ,x∈(0,4),当x=a时,f(x)取得最小值b,则在直角坐标系中函数g(x)=
,x∈(0,4),当x=a时,f(x)取得最小值b,则在直角坐标系中函数g(x)= 的图象为( )
的图象为( )



 的部分图象大致是 ( )
的部分图象大致是 ( )
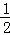 ;其中,所有正确结论的序号是 ;
;其中,所有正确结论的序号是 ; },B={
},B={ },且A∩B=A,则
},且A∩B=A,则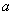 的所有值组成的集合是( )
的所有值组成的集合是( ) B.
B. C.{
C.{ ,
, } D.{
} D.{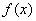 ,若存在区间
,若存在区间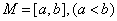 ,使得
,使得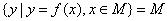 ,则称区间M为函数
,则称区间M为函数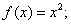 ②
②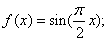 ③
③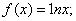 ④
④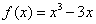
 ,且
,且 若
若 则集合
则集合 最多会有_ __个子集.
最多会有_ __个子集.