题目内容
为研究学生喜爱打篮球是否与性别有关,某兴趣小组对本班48名同学进行了问卷调查,得到了如下列联表:
若在全班48名同学中随机抽取一人为喜爱打篮球的同学的概率为
.
(Ⅰ)请将列联表补充完整(不用写计算过程);
(Ⅱ)你是否有95%的把握认为喜爱打篮球与性别有关?说明理由;
(Ⅲ)若从女同学中抽取2人进一步调查,设其中喜爱打篮球的女同学人数为X,求X的分布列与期望.
附:K2=
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 6 | ||
| 女生 | 10 | ||
| 合计 | 48 |
| 2 |
| 3 |
(Ⅰ)请将列联表补充完整(不用写计算过程);
(Ⅱ)你是否有95%的把握认为喜爱打篮球与性别有关?说明理由;
(Ⅲ)若从女同学中抽取2人进一步调查,设其中喜爱打篮球的女同学人数为X,求X的分布列与期望.
附:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
考点:独立性检验的应用
专题:应用题,概率与统计
分析:(Ⅰ)根据在全部48人中随机抽取1人抽到喜爱打篮球的学生的概率,做出喜爱打篮球的人数,进而做出男生的人数,填好表格.
(Ⅱ)根据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看出有多大的把握说明打篮球和性别有关系.
(Ⅲ)喜爱打篮球的女生人数ξ的可能取值为0,1,2,通过列举得到事件数,分别计算出它们的概率,最后利用列出分布列,求出期望即可.
(Ⅱ)根据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看出有多大的把握说明打篮球和性别有关系.
(Ⅲ)喜爱打篮球的女生人数ξ的可能取值为0,1,2,通过列举得到事件数,分别计算出它们的概率,最后利用列出分布列,求出期望即可.
解答:
解:(Ⅰ)列联表补充如下:----------------------------------------(3分)
(Ⅱ)∵K2=
≈4.286>3.841------------------------(5分)
∴有95%的把握认为喜爱打篮球与性别有关.---------------------(6分)
(Ⅲ)喜爱打篮球的女生人数ξ的可能取值为0,1,2.-------------------------(7分)
其概率分别为P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
--------------------------(10分)
故ξ的分布列为:
--------------------------(11分)
ξ的期望值为:Eξ=0×
+1×
+2×
=1--------------------(12分)
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 22 | 6 | 28 |
| 女生 | 10 | 10 | 20 |
| 合计 | 32 | 16 | 48 |
| 48×(22×10-10×6)2 |
| 32×16×28×20 |
∴有95%的把握认为喜爱打篮球与性别有关.---------------------(6分)
(Ⅲ)喜爱打篮球的女生人数ξ的可能取值为0,1,2.-------------------------(7分)
其概率分别为P(ξ=0)=
| ||||
|
| 9 |
| 38 |
| ||||
|
| 10 |
| 19 |
| 9 |
| 38 |
--------------------------(10分)
故ξ的分布列为:
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
ξ的期望值为:Eξ=0×
| 9 |
| 38 |
| 10 |
| 19 |
| 9 |
| 38 |
点评:本题是一个统计综合题,包含独立性检验、离散型随机变量的期望与方差和概率,本题通过创设情境激发学生学习数学的情感,帮助培养其严谨治学的态度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
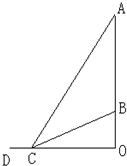 如图,AB表示一座塑像,OB是塑像底座,塑像及其底座所在直线与地面垂直,已知AB=9m,OB=3m.
如图,AB表示一座塑像,OB是塑像底座,塑像及其底座所在直线与地面垂直,已知AB=9m,OB=3m. 前不久,社科院发布了2013年度“全国城市居民幸福指数排行榜”,北京市称为本年度最“幸福城”.随后,某师大附中学生会组织部分同学,用“10份制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.
前不久,社科院发布了2013年度“全国城市居民幸福指数排行榜”,北京市称为本年度最“幸福城”.随后,某师大附中学生会组织部分同学,用“10份制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.