题目内容
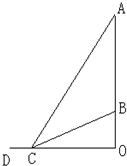 如图,AB表示一座塑像,OB是塑像底座,塑像及其底座所在直线与地面垂直,已知AB=9m,OB=3m.
如图,AB表示一座塑像,OB是塑像底座,塑像及其底座所在直线与地面垂直,已知AB=9m,OB=3m.(1)请用∠ACO与∠BCO的正切表示∠ACB的正切;
(2)在地面OD上求一点C,使C对塑像AB的视角∠ACB最大,这时OC长多少?
考点:两角和与差的正切函数
专题:三角函数的求值
分析:(1)由图得∠ACB=∠ACO-∠BCO,代入两角差的正切公式即可;
(2)设OC=x米,∠ACB=θ,求出x和θ的范围,利用(1)的结论和正切函数的定义表示出tan∠ACB,即tanθ,
化简后利用基本不等式求出最大值和此时的x,根据正切函数的单调性值此时θ也最大.
(2)设OC=x米,∠ACB=θ,求出x和θ的范围,利用(1)的结论和正切函数的定义表示出tan∠ACB,即tanθ,
化简后利用基本不等式求出最大值和此时的x,根据正切函数的单调性值此时θ也最大.
解答:
解:(1)由图得,∠ACB=∠ACO-∠BCO,
则tan∠ACB=tan(∠ACO-∠BCO)=
…(3分)
(2)设OC=x米,x>0,∠ACB=θ,且θ∈(0,
),
如图,tan∠ACD=
=
,tan∠BCD=
=
,(5分)
则tan∠ACB=tanθ=
=
=
≤
=
=
,
当且仅当x=
时,即x=6时取等号,(8分)
∵θ∈(0,
),且y=tanθ是增函数,∴x=6时,tanθ最大,θ也最大,
答:当CO=6米时,C对塑像AB的视角∠ACB最大.(10分)
则tan∠ACB=tan(∠ACO-∠BCO)=
| tan∠ACO-tan∠BCO |
| 1+tan∠ACO•tan∠BCO |
(2)设OC=x米,x>0,∠ACB=θ,且θ∈(0,
| π |
| 2 |
如图,tan∠ACD=
| AO |
| CO |
| 12 |
| x |
| BO |
| CO |
| 3 |
| x |
则tan∠ACB=tanθ=
| ||||
1+
|
| ||
1+
|
| 9 | ||
x+
|
| 9 | ||||
2
|
| 9 | ||
2
|
| 3 |
| 4 |
当且仅当x=
| 36 |
| x |
∵θ∈(0,
| π |
| 2 |
答:当CO=6米时,C对塑像AB的视角∠ACB最大.(10分)
点评:本题考查两角差的正切函数,正切函数的定义、单调性的实际应用,把角最大的问题转化为角的正切值最大,考查转化思想.

练习册系列答案
相关题目
