题目内容
10.设函数f(x)=${log}_{3}^{2}x+3l{og}_{3}x+2$,且$\frac{1}{9}$≤x≤9.(1)求f(3)的值;
(2)求函数f(x)的最大值与最小值及与之对应的x的值.
分析 (1)直接利用函数的解析式,通过对数运算法则求解函数值即可.
(2)利用换元法,结合x的范围,求出换元的范围,利用二次函数的最值求解函数的最值以及与之对应的x的值.
解答 解:(1)函数f(x)=${log}_{3}^{2}x+3l{og}_{3}x+2$,且$\frac{1}{9}$≤x≤9.
f(3)=log323+3log33+2=1+3+2=6.
(2)令t=log3x,f(x)=${log}_{3}^{2}x+3l{og}_{3}x+2$=t2+3t+2,又$\frac{1}{9}$≤x≤9,-2≤log3x≤2,
∴-2≤t≤2,令g(t)=t2+3t+2=(t+$\frac{3}{2}$)2-$\frac{1}{4}$,t∈[-2,2],
当t=$-\frac{3}{2}$时,g(t)min=-$\frac{1}{4}$,即log3x=-$\frac{3}{2}$,可得x=${3}^{-\frac{3}{2}}$=$\frac{\sqrt{3}}{9}$.
∴f(x)min=-$\frac{1}{4}$,此时x=$\frac{\sqrt{3}}{9}$.
当t=2时,g(t)max=g(2)=12,即log3x=2,可得x=9,
∴f(x)max=12,此时x=9.
点评 本题考查函数值的求法,二次函数的最值的求法,换元法的应用,考查计算能力以及转化思想的应用.

练习册系列答案
相关题目
16.要得到函数y=2sin(2x+$\frac{π}{4}$)的图象,只需将函数y=2sin(x+$\frac{π}{4}$)的图象( )
| A. | 在纵坐标不变时,横坐标伸长到原来的2倍 | |
| B. | 在纵坐标不变时,横坐标缩短到原来的$\frac{1}{2}$倍 | |
| C. | 在横坐标不变时,纵坐标伸长到原来的2倍 | |
| D. | 在横坐标不变时,纵坐标缩短到原来的$\frac{1}{2}$倍 |
19.已知x0=$\frac{π}{3}$是函数f(x)=sin(2x+φ)(|φ|<$\frac{π}{2}$)的一个极大值点,则f(x)的一个单调递减区间是( )
| A. | ($\frac{π}{3}$,$\frac{5π}{6}$) | B. | ($\frac{π}{6}$,$\frac{5π}{6}$) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{2π}{3}$,π) |
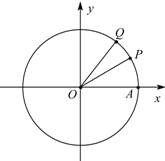 如图,设A是单位圆和x轴正半轴的交点,P、Q是单位圆上的两点,O是坐标原点,∠AOP=$\frac{π}{6}$,∠AOQ=α,α∈[0,π).
如图,设A是单位圆和x轴正半轴的交点,P、Q是单位圆上的两点,O是坐标原点,∠AOP=$\frac{π}{6}$,∠AOQ=α,α∈[0,π).