题目内容
4.已知A,B是圆O:x2+y2=4上的两个动点,P是线段A,B上的动点,当△AOB的面积最大时,$\overrightarrow{AO}•\overrightarrow{AP}-{\overrightarrow{AP}^2}$的最大值为$\frac{1}{2}$.分析 由题意知当∠AOB=$\frac{π}{2}$时,S取最大值2,此时OA⊥OB建立坐标系可得A、B、P的坐标,可得$\overrightarrow{AO}•\overrightarrow{AP}-{\overrightarrow{AP}^2}$为关于x的二次函数,由二次函数的最值可得.
解答 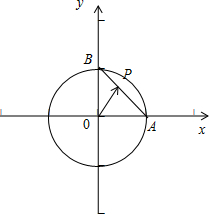 解:由题意知:△AOB的面积S=$\frac{1}{2}|OA||OB|$sin∠AOB
解:由题意知:△AOB的面积S=$\frac{1}{2}|OA||OB|$sin∠AOB
=$\frac{1}{2}$×2×2×sin∠AOB=2sin∠AOB,
当∠AOB=$\frac{π}{2}$时,S取最大值2,此时OA⊥OB,
如图所示,不妨取A(2,0),B(0,2),设P(x,2-x)
∴$\overrightarrow{AO}•\overrightarrow{AP}-{\overrightarrow{AP}^2}$=$\overrightarrow{AP}•\overrightarrow{PO}$
=(x-2,2-x)•(-x,x-2)
=-x(x-2)+(2-x)(x-2)
=(x-2)(2-2x)=-2x2+6x-1,x∈[0,2]
当x=$\frac{3}{2}$时,上式取最大值$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查平面向量的数量积的运算,涉及三角形的面积公式和二次函数的最值,属中档题.

练习册系列答案
相关题目
12.四棱锥P-ABCD的底面是边长为2$\sqrt{2}$的正方形,高为1.其外接球半径为2$\sqrt{2}$,则正方形ABCD的中心与点P之间的距离为( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$或1 | D. | 2$\sqrt{2}$或$\sqrt{2}$ |
19.在平面直角坐标系xOy中,已知点A(2,0),直线l:x+y-5=0,点B(x,y)是圆C:x2+2x+y2-1=0上的动点,AD⊥l,BE⊥l,垂足分别为D,E,则线段DE的最大值是( )
| A. | $\sqrt{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $2\sqrt{2}$ | D. | $\frac{{5\sqrt{2}}}{2}$ |
 如图,在直三棱柱ADF-BCE中,AB=BC=BE=2,CE=$2\sqrt{2}$.
如图,在直三棱柱ADF-BCE中,AB=BC=BE=2,CE=$2\sqrt{2}$. 上为增函数的是( )
上为增函数的是( ) B.
B.
 D.
D.