题目内容
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点(1)求证:直线MO∥平面PAB;
(2)求证:平面PCD⊥平面ABM.
(3)求直线PB与平面ABM所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)分别取线段AB、PA的中点E、F,证明MO∥FE,即可证明直线MO∥平面PAB;
(2)证明平面PCD⊥平面ANM,只需证明AM⊥平面PCD,只需证明CD⊥平面PAD;
(3)证明PM⊥平面ABM,可得∠PBM为直线PB与平面ABM所成角,从而可求直线PB与平面ABM所成角的正弦值.
(2)证明平面PCD⊥平面ANM,只需证明AM⊥平面PCD,只需证明CD⊥平面PAD;
(3)证明PM⊥平面ABM,可得∠PBM为直线PB与平面ABM所成角,从而可求直线PB与平面ABM所成角的正弦值.
解答:
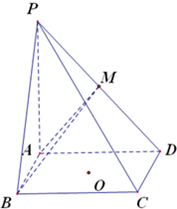 (1)证明:分别取线段AB、PA的中点E、F,则FM∥AD,EO∥AD,所以FM∥EO,
(1)证明:分别取线段AB、PA的中点E、F,则FM∥AD,EO∥AD,所以FM∥EO,
又|FM|=
|AD|=|EO|,所以四边形FMOE为平行四边形,
所以MO∥FE,
又FE?平面PAB,MO?平面PAB,
所以直线MO∥平面PAB(5分)
(2)证明:因为PA⊥平面ABCD,所以PA⊥CD,
又CD⊥AD,PA∩AD=A,
所以CD⊥平面PAD,
所以CD⊥AM,
又AM⊥PD,CD∩PD=D,
所以AM⊥平面PCD,
又AM?平面ABM,
所以平面PCD⊥平面ABM; (10分)
(3)解:由(2)知,PM⊥AM,PM⊥AB,
因为AM∩AB=A,
所以PM⊥平面ABM,
所以∠PBM为直线PB与平面ABM所成角.
令|AB|=1,则|PM|=
,|PB|=
,
所以sin∠PBM=
=
(15分)
 (1)证明:分别取线段AB、PA的中点E、F,则FM∥AD,EO∥AD,所以FM∥EO,
(1)证明:分别取线段AB、PA的中点E、F,则FM∥AD,EO∥AD,所以FM∥EO,又|FM|=
| 1 |
| 2 |
所以MO∥FE,
又FE?平面PAB,MO?平面PAB,
所以直线MO∥平面PAB(5分)
(2)证明:因为PA⊥平面ABCD,所以PA⊥CD,
又CD⊥AD,PA∩AD=A,
所以CD⊥平面PAD,
所以CD⊥AM,
又AM⊥PD,CD∩PD=D,
所以AM⊥平面PCD,
又AM?平面ABM,
所以平面PCD⊥平面ABM; (10分)
(3)解:由(2)知,PM⊥AM,PM⊥AB,
因为AM∩AB=A,
所以PM⊥平面ABM,
所以∠PBM为直线PB与平面ABM所成角.
令|AB|=1,则|PM|=
| 2 |
| 5 |
所以sin∠PBM=
| ||
|
| ||
| 5 |
点评:本题考查线面平行、线面垂直,考查面面垂直,考查线面角,考查学生分析解决问题的能力,考查学生的计算能力,正确运用线面平行、面面垂直的判定定理是关键.

练习册系列答案
相关题目
在△ABC中,AB=BC=3,∠ABC=30°,AD是边BC上的高,则|
•
|的值等于( )
| AD |
| AC |
| A、0 | ||
B、
| ||
| C、4 | ||
D、-
|
若等差数列的首项是-24,且从第10项开始大于零,则公差d的取值范围是( )
A、d>
| ||
| B、d<3 | ||
C、
| ||
D、
|