题目内容
若等差数列的首项是-24，且从第10项开始大于零，则公差d的取值范围是（ ）
A、d＞
| ||
| B、d＜3 | ||
C、
| ||
D、
|
考点：等差数列的性质
专题：等差数列与等比数列
分析：直接写出等差数列的通项公式，由a9≤0且a10＞0联立不等式组求得公差d的取值范围．
解答：
解：∵等差数列的首项是-24，
则等差数列的通项公式为an=-24+（n-1）d，
要使从第10项开始为正，
则由
，解得：
＜d≤3．
故选：D．
则等差数列的通项公式为an=-24+（n-1）d，
要使从第10项开始为正，
则由
|
| 8 |
| 3 |
故选：D．
点评：本题考查了等差数列的性质，关键是明确从第10项开始大于零的含义，是中低档题．
练习册系列答案
相关题目
如图，在四棱锥P-ABCD中，底面ABCD是矩形，O为底面中心，PA⊥平面ABCD，PA=AD=2AB．M是PD的中点
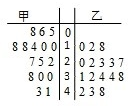甲乙两组统计数据用茎叶图表示，设甲乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=2sin（2x+
）的图象向左平移φ（φ＞0）个单位后所得的图象关于y轴对称，则φ的最小值为（ ）
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
等比数列{an}中，a1+a2=8，a3-a1=16，则a3等于（ ）
| A、20 | B、18 | C、10 | D、8 |