题目内容
11．若z1=a+2i，z2=3-4i，且$\frac{z_1}{z_2}$为虚数，则a的范围是a≠$-\frac{3}{2}$．分析 利用复数的运算法则、共轭复数的定义、虚数的定义即可得出．
解答 解：$\frac{z_1}{z_2}$=$\frac{a+2i}{3-4i}$=$\frac{（a+2i）（3+4i）}{（3-4i）（3+4i）}$=$\frac{3a-8+（6+4a）i}{25}$为虚数，
∴$\frac{6+4a}{25}$≠0，
解得a≠$-\frac{3}{2}$．
故答案为：$a≠-\frac{3}{2}$．
点评 本题考查了复数的运算法则、共轭复数的定义、虚数的定义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
19．已知f（x）=$\left\{\begin{array}{l}{x+3，x≤1}\\{-{x}^{2}+2x+3，x＞1}\end{array}\right.$，则使得f（x）-ex-m≤0恒成立的m的取值范围是（ ）
| A． | （-∞，2） | B． | （-∞，2] | C． | （2，+∞） | D． | [2，+∞） |
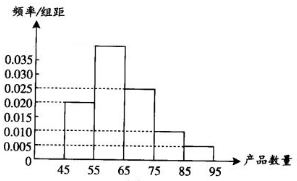为了调查某厂工人生产某种产品的能力，随机抽查了20位工人某天生产该产品的数量．产品数量的分组区间为[45，55），[55，65），[65，75），[75，85），[85，95）由此得到频率分布直方图如图．则产品数量位于[55，65）范围内的频率为0.4；这20名工人中一天生产该产品数量在[55，75）的人数是13．