题目内容
5.若点A的坐标是(3,2),F是抛物线y2=2x的焦点,点P在抛物线上移动,为使得|PA|+|PF|取得最小值,则P点的坐标是( )| A. | (1,2) | B. | (2,1) | C. | (2,2) | D. | (0,1) |
分析 将PF的长度转化为P到准线的距离.
解答 解:由P向准线x=-$\frac{1}{2}$作垂线,垂足为M,由抛物线的定义,PF=PM,再由定点A向准线作垂线,垂足为N,那么点P在该抛物线上移动时,有PA+PF=PA+PM≥AN,当且仅当A,P,N三点共线时取得最小值AN=3-(-$\frac{1}{2}$)=$\frac{7}{2}$,此时P的纵坐标为2,横坐标为2.
P点的坐标是:(2,2).
故选:C.
点评 本体着重考查抛物线的定义,即它的几何本质.基于此知识的基础上,进行转化求的.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
16.设函数f(x)和g(x)分别是R上的奇函数和偶函数,则函数h(x)=g(x)|f(x)|的图象(( )
| A. | 关于原点对称 | B. | 关于x轴对称 | C. | 关于y轴对称 | D. | 关于直线y=x对称 |
13.阅读程序框图,如果输出的函数值在区间[1,3]上,则输入的实数x的取值范围是( )
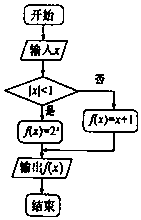

| A. | [0,2] | B. | [0,1] | C. | [-1,1) | D. | (-1,2] |
10.已知α,β是两个不同平面,直线l?β,则“α∥β”是“l∥α”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |