题目内容
18.函数$f(x)=\sqrt{-{x^2}+(a+2)x-a-1}(a>0)$的定义域为集合A,函数g(x)=2x-1(x≤2)的值域为集合B.(1)当a=1时,求集合A,B;
(2)若集合A,B满足A∪B=B,求实数a的取值范围.
分析 (1)根据a=1,可得-x2+3x-2≥0,即x2-3x+2≤0,可求x的范围,得到集合A,根据指数的性质,可得值域,得到集合B.
(2)根据A∪B=B,即A⊆B,建立条件关系即可求实数a的取值范围.
解答 解:(1)当a=1时,由题意得-x2+3x-2≥0,即x2-3x+2≤0,
解得:1≤x≤2,
∴集合A=[1,2],
由函数g(x)=2x-1(x≤2),可知函数g(x)在(-∞,2]上单调递增,
∴-1≤2x-1≤3,
∴集合B=(-1,3].
(2)∵A∪B=B,
∴A⊆B,
由题意得-x2+(a+2)x-a-1≥0
得x2-(a+2)x+a+1≤0,即(x-1)[x-(a+1)]≤0,
由方程(x-1)[x-(a+1)]=0,
可得:x1=1,x2=a+1
∵a>0,
∴不等式的解集为[1,a+1],即集合A=[1,a+1],
由A⊆B,
∴a+1≤3,
∴a≤2,
故得实数a的取值范围是{a|0<a≤2}.
点评 本题主要考查不等式的计算以及集合的基本运算,属于基础题.

练习册系列答案
相关题目
8.已知f′(x)是定义在(0,+∞)上的函数f(x)的导函数,若方程f′(x)=0无解,且?x∈(0,+∞),f[f(x)-log2016x]=2017,设a=f(20.5),b=f(logπ3),c=f(log43),则a,b,c的大小关系是( )
| A. | b>c>a | B. | a>c>b | C. | c>b>a | D. | a>b>c |
6.已知函数f(x)为定义在R上的奇函数,当x>1时,f(x)=2x-8x-f(2),则当x<-1时,f(x)的表达式为( )
| A. | f(x)=-2-x-8x-6 | B. | f(x)=-2-x-8x+6 | C. | f(x)=2-x+8x+6 | D. | f(x)=-2-x+8x-6 |
13.阅读程序框图,如果输出的函数值在区间[1,3]上,则输入的实数x的取值范围是( )
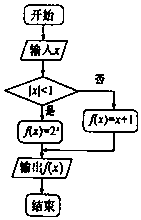

| A. | [0,2] | B. | [0,1] | C. | [-1,1) | D. | (-1,2] |
3.下列函数中,最小值为4的是( )
| A. | y=x+$\frac{4}{x}$ | B. | y=sinx+$\frac{4}{sinx}$(0<x<π) | ||
| C. | y=ex+4e-x | D. | y=log3x+4logx3 |
10.已知α,β是两个不同平面,直线l?β,则“α∥β”是“l∥α”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |