题目内容

13．已知函数f（x）=$\frac{a}{x-a}$在区间（3，+∞）上单调递减，则a的取值范围是（0，3）．

分析 根据反比例函数y=$\frac{k}{x}$在k＞0时的单调性，结合题意，即可求出a的取值范围．

解答 解：∵函数f（x）=$\frac{a}{x-a}$在区间（3，+∞）上单调递减，
∴$\left\{\begin{array}{l}{a＞0}\\{3-a＞0}\end{array}\right.$，
解得3＞a＞0．
故答案为：（0，3）．

点评 本题考查了反比例类型的函数单调性问题，是基础题目．

练习册系列答案
相关题目
3．已知等差数列{an}中，a1=4，a2=6，则S4=（　　）
A．18B．21C．28D．40
4．已知函数f（x）=cos2x+asinx（a∈R），
（Ⅰ）若a=6，求f（x）的最大值及此时x的值；
（Ⅱ）若函数f（x）在区间[$\frac{π}{6}$，$\frac{π}{2}$]上的最小值为4，求实数a的值．
1．某公司电脑专业技术人员对该公司A，B两个办公室的50台电脑进行报废检查，其中A办公室的电脑占60%，B办公室的电脑占40%，A办公室电脑的报废率为10%，B办公室电脑的报废率为20%．
（1）若从这50台电脑中随机抽取1台（每台电脑被抽到的机会相等），求该电脑是A办公室的且不报废的概率．
（2）若从这50台电脑中随机抽取2台（每台电脑被袖到的机会相等），记这2台电脑是A办公室的且不报废的台数为ξ，求ξ的分布列与数学期望．
8．已知命题p：x2-ax+1=0有两个实根，q：函数y=x2+ax+b在[1，+∞）上为增函数，若命题“p∧q”为真命题，求实数a的取值范围．
18．若f（x）=$\left\{\begin{array}{l}{{x}^{2}+2，x≥0}\\{2x+3，x＜0}\end{array}\right.$，则f（-1）=1．
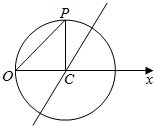5．在极坐标系中，已知圆C经过点P（$\sqrt{2}$，$\frac{π}{4}$），圆心为直线$ρsin（θ-\frac{π}{3}）$=-$\frac{\sqrt{3}}{2}$与极轴的交点，求圆C的直角坐标方程．
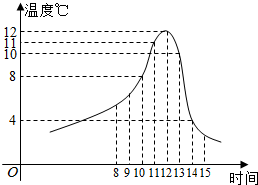2．$\overrightarrow{AB}$+$\overrightarrow{AC}$+$\overrightarrow{CB}$-$\overrightarrow{BA}$=3$\overrightarrow{AB}$．
3．某食品的保鲜时间t（单位：小时）与储藏温度x（单位：℃）满足函数关系t=$\left\{\begin{array}{l}{64，x≤0}\\{{2}^{kx+6}，x＞0}\end{array}\right.$且该食品在4℃的保鲜时间是16小时．已知甲在某日上午10时购买了该食品，并将其遗放在室外，且此日的室外温度随时间变化如图所示，给出以下四个结论：
①该食品在6℃的保鲜时间是8小时；
②当x∈[-6，6]时，该食品的保鲜时间t随看x增大而逐渐减少；
③到了此日13时，甲所购买的食品还在保鲜时间内；
④到了此日14时，甲所购买的食品已然过了保鲜时间
其中，所有正确结论的序号是①④．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网