题目内容
1．函数f（x）=$\frac{xln\frac{1}{|x|}}{|x|}$的图象可能是（ ）| A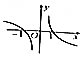． |  | B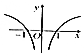． |  | C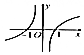． |  | D． |  |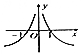
分析 判断函数的奇偶性，排除选项，然后利用特殊值判断求解即可．
解答 解：函数f（x）=$\frac{xln\frac{1}{|x|}}{|x|}$是奇函数，排除选项B，D，
当x=2时，f（2）=$\frac{2ln\frac{1}{2}}{2}$=$ln\frac{1}{2}＜0$，排除C，
故选：A．
点评 本题考查函数的图象的判断，注意函数的奇偶性以及特殊值的应用，是基础题．
练习册系列答案
相关题目
11．
如图正四面体（所有棱长都相等）D-ABC中，动点P在平面BCD上，且满足∠PAD=30°，若点P在平面ABC上的射影为P′，则sin∠P′AB的最大值为（ ）
如图正四面体（所有棱长都相等）D-ABC中，动点P在平面BCD上，且满足∠PAD=30°，若点P在平面ABC上的射影为P′，则sin∠P′AB的最大值为（ ）| A． | $\frac{2\sqrt{7}}{7}$ | B． | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{1}{2}$ |
12．函数f（x）=2-x+1-x的零点所在区间为（ ）
| A． | （-1，0） | B． | （0，1） | C． | （1，2） | D． | （2，3） |
9．函数f（x）=$\sqrt{lo{g}_{\frac{1}{2}}（2x+1）}$的定义域为（ ）
| A． | （-$\frac{1}{2}$，0） | B． | （-$\frac{1}{2}$，0] | C． | （-$\frac{1}{2}$，+∞） | D． | （0，+∞） |
6．
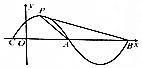函数y=sin（$\frac{π}{2}$x+φ）（|φ|＜$\frac{π}{2}$）的部分图象如图所示，其中P是图象的最高点，A、B是图象与x轴的交点，则tan∠APB=（ ）
函数y=sin（$\frac{π}{2}$x+φ）（|φ|＜$\frac{π}{2}$）的部分图象如图所示，其中P是图象的最高点，A、B是图象与x轴的交点，则tan∠APB=（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{2}$ |
13．设集合A={x|2x-2＜1}，B={x|1-x≥0}，则A∩B等于（ ）
| A． | {x|0＜x≤1} | B． | {x|1≤x＜2} | C． | {x|x≤1} | D． | {x|0＜x＜1} |