题目内容
11. 如图正四面体(所有棱长都相等)D-ABC中,动点P在平面BCD上,且满足∠PAD=30°,若点P在平面ABC上的射影为P′,则sin∠P′AB的最大值为( )
如图正四面体(所有棱长都相等)D-ABC中,动点P在平面BCD上,且满足∠PAD=30°,若点P在平面ABC上的射影为P′,则sin∠P′AB的最大值为( )| A. | $\frac{2\sqrt{7}}{7}$ | B. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
分析 由题意可知:当点P取线段CD的中点时,可得到∠P′AB的最大,并且得到sin∠P′AB的最大值.过D作DO⊥平面ABC,可得点O是等边三角形的中心,连接CO延长与AB相交于点M,CM⊥AB.经过点P作PP′⊥CO,垂足为点P′,则PP′⊥平面ABC,点P′为点P在平面ABC的射影,则点P′为CO的中点.进而得出答案.
解答 解:由题意可知:当点P取线段CD的中点时,可得到∠P′AB的最大,并且得到sin∠P′AB的最大值.
过D作DO⊥平面ABC,则点O是等边三角形的中心,连接CO延长与AB相交于点M,CM⊥AB.经过点P作PP′⊥CO,垂足为点P′,则PP′⊥平面ABC,点P′为点P在平面ABC的射影,则点P′为CO的中点.
不妨取AB=2,则MP′=$\frac{2}{3}×\sqrt{3}$,∴AP′=$\sqrt{{1}^{2}+(\frac{2\sqrt{3}}{3})^{2}}$=$\frac{\sqrt{21}}{3}$.
sin∠P′AM=$\frac{\frac{2\sqrt{3}}{3}}{\frac{\sqrt{21}}{3}}$=$\frac{2\sqrt{7}}{7}$.
故选:A.
点评 本题考查了正四面体的性质、线面垂直的判定与性质定理、等边三角形的性质、空间角,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
2.若函数f(x)=x|x-a|在[2,+∞)上单调递增,则实数a的取值范围为( )
| A. | (-∞,+∞) | B. | (-2,+∞) | C. | (0,+∞) | D. | (-∞,2] |
6.过点P(1,3)的动直线与抛物线y=x2交于A,B两点,在A,B两点处的切线分别为l1、l2,若l1和l2交于点Q,则圆x2+(y-2)2=4上的点与动点Q距离的最小值为$\sqrt{5}$-2.
16.如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log3(x+1)的解集是( )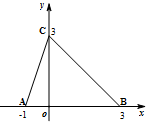

| A. | {x|-1≤x≤2} | B. | {x|-1<x≤2} | C. | {x|-1<x≤0} | D. | {x|-1<x≤3} |
20.在△ABC中,cosA=$\frac{3}{5}$,且sinB=$\frac{12}{13}$,则cosC=( )
| A. | -$\frac{33}{65}$ | B. | $\frac{33}{65}$ | C. | $\frac{63}{65}$ | D. | $\frac{63}{65}$或$\frac{33}{65}$ |