题目内容
设函数f(x)=
的反函数为y=f-1(x)
(1)数列{an}满足f-1(n)•an=3n,求数列{an}的前n项和Sn;
(2)数列{bn}中,bn=2 an,证明数列{bn}为等比数列.
| x |
| 1+x |
(1)数列{an}满足f-1(n)•an=3n,求数列{an}的前n项和Sn;
(2)数列{bn}中,bn=2 an,证明数列{bn}为等比数列.
考点:等比关系的确定,反函数
专题:函数的性质及应用,等差数列与等比数列
分析:(1)求反函数可得f-1(x)=
,代入已知可得an的式子,可判为等差数列,代入求和公式可得;
(2)由(1)知an=3-3n,可得bn=2 an=23-3n,可得
为常数,即可证明.
| x |
| 1-x |
(2)由(1)知an=3-3n,可得bn=2 an=23-3n,可得
| bn+1 |
| bn |
解答:
解:(1)记f(x)=y=
,则可得x=
,
故可得y=f-1(x)=
,f-1(n)=
,
∵f-1(n)•an=3n,∴an=
=3-3n
∴数列{an}是以0为首项,-3为公差的等差数列,
∴Sn=na1+
d=-
n2+
n
(2)由(1)知an=3-3n,
∴bn=2 an=23-3n
∴
=
=2-3=
∴数列{bn}是
为公比的等比数列.
| x |
| 1+x |
| y |
| 1-y |
故可得y=f-1(x)=
| x |
| 1-x |
| n |
| 1-n |
∵f-1(n)•an=3n,∴an=
| 3n |
| f-1(n) |
∴数列{an}是以0为首项,-3为公差的等差数列,
∴Sn=na1+
| n(n-1) |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
(2)由(1)知an=3-3n,
∴bn=2 an=23-3n
∴
| bn+1 |
| bn |
| 23-3(n+1) |
| 23-3n |
| 1 |
| 8 |
∴数列{bn}是
| 1 |
| 8 |
点评:本题考查反函数,涉及等差数列和等比数列的应用,属基础题.

练习册系列答案
相关题目
已知公比为q的等比数列{an}的前n项和为Sn,n∈N*,则下列结论中:
(1)Sn,S2n-Sn,S3n-S2n成等比数列;
(2)(S2n-Sn)2=Sn(S3n-S2n);
(3)S3n-S2n=qn(S2n-Sn)
正确的结论为( )
(1)Sn,S2n-Sn,S3n-S2n成等比数列;
(2)(S2n-Sn)2=Sn(S3n-S2n);
(3)S3n-S2n=qn(S2n-Sn)
正确的结论为( )
| A、(1)(2) |
| B、(1)(3) |
| C、(2)(3) |
| D、(1)(2)(3) |
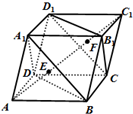 已知平行六面体ABCD-A1B1C1D1,AC1与平面A1BD,CB1D1交于E,F两点.给出以下命题,其中真命题有
已知平行六面体ABCD-A1B1C1D1,AC1与平面A1BD,CB1D1交于E,F两点.给出以下命题,其中真命题有