题目内容
在同一坐标系中,画出函数y=sinx和函数y=tanx在x∈[0,2π]的图象,并根据图象回答下列问题:
(1)写出这两个函数图象的交点坐标;
(2)写出使tanx>sinx成立的x的取值范围;
(3)写出使tanx=sinx成立的x的取值范围;
(4)写出使tanx<sinx成立的x的取值范围;
(5)写出使这两个函数具有相同的单调性的区间.
(1)写出这两个函数图象的交点坐标;
(2)写出使tanx>sinx成立的x的取值范围;
(3)写出使tanx=sinx成立的x的取值范围;
(4)写出使tanx<sinx成立的x的取值范围;
(5)写出使这两个函数具有相同的单调性的区间.
考点:正弦函数的图象,正切函数的图象
专题:三角函数的图像与性质
分析:作出函数y=sinx和函数y=tanx在x∈[0,2π]的图象,根据图象即可得到相应的结论.
解答:
解: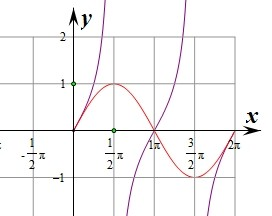 作出函数y=sinx和函数y=tanx在x∈[0,2π]的图象如图:
作出函数y=sinx和函数y=tanx在x∈[0,2π]的图象如图:
(1)则这两个函数图象的交点坐标为(0,0),(π,0),(2π,0);
(2)使tanx>sinx成立的x的取值范围为(0,
)∪(π,
);
(3)使tanx=sinx成立的x的取值范围{x|x=0或x=π或x=2π};
(4)使tanx<sinx成立的x的取值范围(
,π)∪(
,2π);
(5)写出使这两个函数具有相同的单调性的区间:
在[0,
)和(
,2π)上函数单调递增.
 作出函数y=sinx和函数y=tanx在x∈[0,2π]的图象如图:
作出函数y=sinx和函数y=tanx在x∈[0,2π]的图象如图:(1)则这两个函数图象的交点坐标为(0,0),(π,0),(2π,0);
(2)使tanx>sinx成立的x的取值范围为(0,
| π |
| 2 |
| 3π |
| 2 |
(3)使tanx=sinx成立的x的取值范围{x|x=0或x=π或x=2π};
(4)使tanx<sinx成立的x的取值范围(
| π |
| 2 |
| 3π |
| 2 |
(5)写出使这两个函数具有相同的单调性的区间:
在[0,
| π |
| 2 |
| 3π |
| 2 |
点评:本题主要考查三角函数的图象和性质,利用数形结合作出两个函数的图象是解决本题的关键,比较基础,考查学生的视图能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
收敛数列与发散数列的和数列( )
| A、一定收敛 | B、可能发散 |
| C、一定发散 | D、可能收敛 |
等差数列{an}的前n项和为Sn,若a2+a4+a6=12,则S7的值是( )
| A、21 | B、24 | C、28 | D、7 |