题目内容
在关于x的不等式x2-(a+1)x+a<0的解集中恰有两个整数,则a的取值范围是( )
| A、(3,4) |
| B、(-2,-1)∪(3,4) |
| C、(3,4] |
| D、[-2,-1)∪(3,4] |
考点:一元二次不等式的解法
专题:分类讨论,不等式的解法及应用
分析:把不等式x2-(a+1)x+a<0化为(x-1)(x-a)<0,讨论a>1,a<1时,求出解不等式的解集,
再根据不等式的解集中恰有两个整数,求出a的取值范围.
再根据不等式的解集中恰有两个整数,求出a的取值范围.
解答:
解:关于x的不等式x2-(a+1)x+a<0可化为
(x-1)(x-a)<0,
当a>1时,解不等式得1<x<a;
当a<1时,解不等式得a<x<1;
∵不等式的解集中恰有两个整数,∴3<a≤4或-2≤a<-1,
∴a的取值范围是[-2,-1)∪(3,4].
故选:D.
(x-1)(x-a)<0,
当a>1时,解不等式得1<x<a;
当a<1时,解不等式得a<x<1;
∵不等式的解集中恰有两个整数,∴3<a≤4或-2≤a<-1,
∴a的取值范围是[-2,-1)∪(3,4].
故选:D.
点评:本题考查了不等式的解法与应用问题,也考查了分类讨论思想的应用问题,是基础题目.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
已知偶函数f(x)在区间(0,+∞)上单调递减,且a=f(-1),b=f(log24),则实数a,b的大小关系时( )
| A、a<b | B、a=b |
| C、a>b | D、不能比较 |
函数y=ax-1的图象一定过点( )
| A、(0,1) |
| B、(1,1) |
| C、(1,0) |
| D、(0,-1) |
已知数列{an}的首项a1=1,且an=an+1+2,则该数列的通项公式是( )
| A、2n-1 | B、2n+1 |
| C、1-2n | D、3-2n |
“p或q为假”是“p且q为假”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
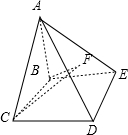 如图,在空间图形A-BCDE中,AB⊥平面BCDE,底面BCDE是直角梯形,且∠CBE=90°,BC∥DE,AB=DE=BE=
如图,在空间图形A-BCDE中,AB⊥平面BCDE,底面BCDE是直角梯形,且∠CBE=90°,BC∥DE,AB=DE=BE=