题目内容
如图所示,长方体ABCD-A1B1C1D1中,BC=CC1=
CD,且E,F,G分别为棱BC,CD,A1B1的中点.
(1)求证:AG∥平面C1EF;
(2)求异面直线AG与C1E所成角的余弦值.

| 1 |
| 2 |
(1)求证:AG∥平面C1EF;
(2)求异面直线AG与C1E所成角的余弦值.

考点:异面直线及其所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,由
=(0,1,1),
=(0,1,1),得AG∥FC1,由此能证明AG∥平面C1EF.
(2)求出
=(0,1,1),
=(
,0,-1),由此利用向量法能求出异面直线AG与C1E所成角的余弦值.
| AG |
| FC1 |
(2)求出
| AG |
| C1E |
| 1 |
| 2 |
解答:
(1)证明: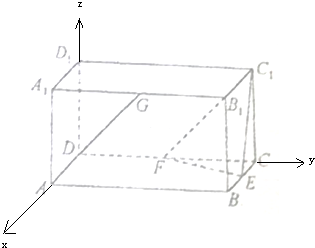 以D为原点,DA为x轴,DC为y轴,DD1为z轴,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,
建立空间直角坐标系,
设BC=CC1=
CD=1,
则A(1,0,0),G(1,1,1),
F(0,1,0),C1=(0,2,1),
∴
=(0,1,1),
=(0,1,1),
∴
∥
,∴AG∥FC1,
又AG?平面C1EF,FC1?平面C1EF,
∴AG∥平面C1EF.
(2)解:
=(0,1,1),E(
,2,0),
=(
,0,-1),
设异面直线AG与C1E所成角为θ,
则cosθ=
=
=
.
∴异面直线AG与C1E所成角的余弦值为
.
 以D为原点,DA为x轴,DC为y轴,DD1为z轴,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设BC=CC1=
| 1 |
| 2 |
则A(1,0,0),G(1,1,1),
F(0,1,0),C1=(0,2,1),
∴
| AG |
| FC1 |
∴
| AG |
| FC1 |
又AG?平面C1EF,FC1?平面C1EF,
∴AG∥平面C1EF.
(2)解:
| AG |
| 1 |
| 2 |
| C1E |
| 1 |
| 2 |
设异面直线AG与C1E所成角为θ,
则cosθ=
|
| ||||
|
|
| 1 | ||||||
|
| ||
| 5 |
∴异面直线AG与C1E所成角的余弦值为
| ||
| 5 |
点评:本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力,解题时要注意向量法的合理运用.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知S、A、B、C是球O表面上的点,SA⊥平面ABC,△ABC为等边三角形,SA=AB=1,则球O的表面积为( )
A、
| ||
B、
| ||
| C、π | ||
D、
|
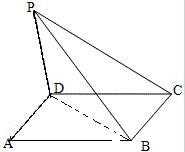 如图,PD⊥平面ABCD,AD⊥PC,AD∥BC,PD:DC:BC=1:1:
如图,PD⊥平面ABCD,AD⊥PC,AD∥BC,PD:DC:BC=1:1: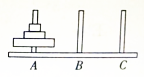 从古印度的汉诺塔传说演变了一个汉诺塔游戏:如图,有三根杆子A、B、C,A杆上有三个碟子(大小不等,自上到下,由小到大),每次移动一个碟子,小的只能叠在大的上面,把所有的碟子从A杆移到C杆上,试设计一个算法,完成上述游戏.
从古印度的汉诺塔传说演变了一个汉诺塔游戏:如图,有三根杆子A、B、C,A杆上有三个碟子(大小不等,自上到下,由小到大),每次移动一个碟子,小的只能叠在大的上面,把所有的碟子从A杆移到C杆上,试设计一个算法,完成上述游戏.