题目内容
7.已知f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(b-1)x2+b2x(b为常数)在x=1处取得极值,则b的值是0.分析 求出f′(x),f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(b-1)x2+b2x(b为常数)在x=1处取得极值,能求出b.
解答 解:∵f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(b-1)x2+b2x
∴f′(x)=x2+(b-1)x+b2,
∵f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$(b-1)x2+b2x(b为常数)在x=1处取得极值,
∴f′(1)=1+(b-1)+b2=0,
解得b=0或b=-1.
当b=-1时,f′(x)=x2-2x+1≥0,在x=1处没有取得极值.
当b=0时,f′(x)=x2-x,在x=1处取得极值.
故答案为:0
点评 本题考查函数的极值的性质的应用,解题时要认真审题,注意导数性质的灵活运用.注意检验.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
18.已知a=0.33,b=30.3,c=0.23,则a,b,c的大小关系为( )
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | c<b<a |
2.函数y=3-x(-2≤x≤1)的值域是( )
| A. | [3,9] | B. | [$\frac{1}{3}$,9] | C. | [$\frac{1}{3}$,3] | D. | [$\frac{1}{9}$,$\frac{1}{3}$] |
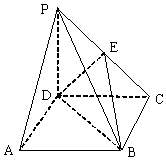 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点.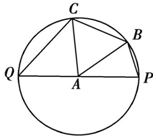 已知PQ是半径为1的圆A的直径,B,C为不同于P,Q的两点,如图所示,记∠PAB=θ.
已知PQ是半径为1的圆A的直径,B,C为不同于P,Q的两点,如图所示,记∠PAB=θ.