题目内容
11.已知函数f(x)=$\frac{1}{2}$ax2-(a+1)x+lnx,其中a>0.(I)讨论函数f(x)的单调性;
(II)若a>1,证明:对任意x1,x2∈(1,+∞)(x1≠x2),总有$\frac{{|f({x_1})-f({x_2})|}}{{|a{x_1}^2-a{x_2}^2|}}$<$\frac{1}{2}$.
分析 (Ⅰ)求导,并判断导数的符号,分别讨论a的取值,确定函数的单调区间.
(Ⅱ)不妨设x1>x2>1,则有f(x1)>f(x2),$a{x_1}^2>a{x_2}^2$,于是要证$\frac{{|f({x_1})-f({x_2})|}}{{|a{x_1}^2-a{x_2}^2|}}<\frac{1}{2}$,即证$f({x_1})-\frac{1}{2}a{x_1}^2<f({x_2})-\frac{1}{2}a{x_2}^2$,构造函数,利用导数和函数的单调性的关系即可证明.
解答 解:( I)∵x∈(0,+∞),$f'(x)=ax-(a+1)+\frac{1}{x}=\frac{(ax-1)(x-1)}{x}$,
令f'(x)=0,得$x=\frac{1}{a}$或x=1.
①若0<a<1,则x∈(0,1)时,f'(x)>0;$x∈(1,\frac{1}{a})$时,f'(x)<0;$x∈(\frac{1}{a},+∞)$时,f'(x)>0,
故函数f(x)在(0,1),$(\frac{1}{a},+∞)$上单调递增,在$(1,\frac{1}{a})$上单调递减.
②若a=1时,则f(x)在(0,+∞)上单调递增.
③若a>1时,则f(x)在$(0,\frac{1}{a})$,(1,+∞)上单调递增,在$(\frac{1}{a},1)$上单调递减.
( II)由( I)可知,当a>1时,f(x)在(1,+∞)上单调递增,
不妨设x1>x2>1,则有f(x1)>f(x2),$a{x_1}^2>a{x_2}^2$,于是要证$\frac{{|f({x_1})-f({x_2})|}}{{|a{x_1}^2-a{x_2}^2|}}<\frac{1}{2}$,
即证$f({x_1})-f({x_2})<\frac{1}{2}a{x_1}^2-\frac{1}{2}a{x_2}^2$,
即证$f({x_1})-\frac{1}{2}a{x_1}^2<f({x_2})-\frac{1}{2}a{x_2}^2$,
令$h(x)=f(x)-\frac{1}{2}a{x^2}=lnx-(a+x)(x>1)$,
∵$h'(x)=\frac{1}{x}-(a+1)=\frac{1-(a+1)x}{x}$,
∵(a+1)x>2,1-(a+1)x<0,
∴h(x)在(1,+∞)上单调递减,即有h(x1)<h(x2).
故对任意x1,x2∈(1,+∞)(x1≠x2),总有$\frac{{|f({x_1})-f({x_2})|}}{{|a{x_1}^2-a{x_2}^2|}}$<$\frac{1}{2}$.
点评 本题主要考查了利用导数研究函数的单调性和求函数的最值问题,体现了分类讨论和转化的思想方法.

| A. | [3,9] | B. | [$\frac{1}{3}$,9] | C. | [$\frac{1}{3}$,3] | D. | [$\frac{1}{9}$,$\frac{1}{3}$] |
| A. | a1+a3≥2a2 | B. | 若a3>a1,则a4>a2 | C. | 若a1=a3,则a1=a2 | D. | a12+a32≥2a22 |

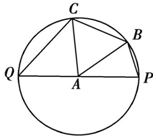 已知PQ是半径为1的圆A的直径,B,C为不同于P,Q的两点,如图所示,记∠PAB=θ.
已知PQ是半径为1的圆A的直径,B,C为不同于P,Q的两点,如图所示,记∠PAB=θ.