题目内容
4.在△ABC中,角A,B,C的对边分别为a,b,c,已知4sin2$\frac{A+B}{2}$-cos2C=$\frac{7}{2}$,且c=$\sqrt{7}$,(1)求角C
(2)求△ABC的面积的最大值.
分析 (1)利用二倍角公式,结合C是三角形的内角,可求C;
(2)利用余弦定理,求得ab的最大值,再利用三角形的面积公式,即可求得结论.
解答 解:(1)∵4sin2$\frac{A+B}{2}$-cos2C=$\frac{7}{2}$,
∴2[1-cos(A+B)]-2cos2C+1=$\frac{7}{2}$,
∴2+2cosC-2cos2C=$\frac{5}{2}$,
∴cos2C-cosC+$\frac{1}{4}$=0,
∴cosC=$\frac{1}{2}$,
∵0<C<π,∴C=$\frac{π}{3}$;
(2)由c=$\sqrt{7}$,
由余弦定理得:cosC=$\frac{{a}^{2}+{b}^{2}-7}{2ab}$,
∴ab=a2+b2-7,
∵a2+b2≥2ab(当且仅当a=b取得等号),
∴ab≥2ab-7,即ab≤7,
即有S△ABC=$\frac{1}{2}$absinC≤$\frac{1}{2}$×7×$\frac{\sqrt{3}}{2}$=$\frac{7\sqrt{3}}{4}$.
当a=b时,△ABC的面积的最大值为$\frac{7\sqrt{3}}{4}$.
点评 本题考查二倍角余弦公式的运用,余弦定理和基本不等式的运用,考查运算能力,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
9.《九章算术》第三章“衰分”介绍比例分配问题:“衰分”是按比例递减分配的意思,通常称递减的比例(即百分比)为“衰分比”.如:甲、乙、丙、丁分别分得100,60,36,21.6,递减的比例为40%,那么“衰分比”就等于40%,今共有粮a(a>0)石,按甲、乙、丙、丁的顺序进行“衰分”,已知丙分得36石,乙、丁所得之和为75石,则“衰分比”与a的值分别是( )
| A. | 75%,$\frac{525}{4}$ | B. | 25%,$\frac{525}{4}$ | C. | 75%,175 | D. | 25%,175 |
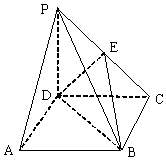 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点.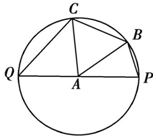 已知PQ是半径为1的圆A的直径,B,C为不同于P,Q的两点,如图所示,记∠PAB=θ.
已知PQ是半径为1的圆A的直径,B,C为不同于P,Q的两点,如图所示,记∠PAB=θ.