题目内容
19.已知函数f(x)=($\frac{1}{2}$)x,a、b∈R+,A=f($\frac{a+b}{2}$),B=f($\sqrt{ab}$),C=f($\frac{ab}{a+b}$),则A、B、C的大小关系是( )| A. | A≤B≤C | B. | A≤C≤B | C. | B≤C≤A | D. | C≤B≤A |
分析 由不等式可证$\frac{a+b}{2}$≥$\sqrt{ab}$≥$\frac{ab}{a+b}$,结合指数函数的单调性可得.
解答 解:∵a、b∈R+,∴$\frac{a+b}{2}$≥$\sqrt{ab}$,$\frac{ab}{a+b}$≤$\frac{ab}{2\sqrt{ab}}$=$\frac{\sqrt{ab}}{2}$≤$\sqrt{ab}$,
又f(x)=($\frac{1}{2}$)x为R上的单调递减函数,
∴f($\frac{a+b}{2}$)≤f($\sqrt{ab}$)≤f($\frac{ab}{a+b}$),即A≤B≤C
故选:A
点评 本题考查基本不等式证明式子大小,涉及指数函数的单调性,属基础题.

练习册系列答案
相关题目
10.对于函数y=f(x)图象上任意一点P(x1,y1),存在Q(x2,y2),使得x1x2+y1y2=0,则函数y=f(x)可以为( )
| A. | y=2x-2 | B. | y=log2x | C. | y=x2+1 | D. | y=x+1 |
14.已知|$\overrightarrow{a}$|=10,|$\overrightarrow{b}$|=12,且$\overrightarrow{a}$•($\frac{1}{2}$$\overrightarrow{b}$)=-30,则$\overrightarrow{a}$和$\overrightarrow{b}$的夹角为( )
| A. | 60° | B. | 120° | C. | 135° | D. | 150° |
4.在正项等比数列{an}中,a1=2,S3=$\frac{26}{9}$,则数列{an}的通项公式为( )
| A. | 2×($\frac{2}{3}$)n-1 | B. | 2×($\frac{1}{3}$)n-1 | C. | 2×($\frac{4}{3}$)n-1 | D. | 2×($\frac{4}{3}$)n |
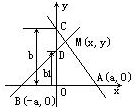 如图,二杆各绕点A(a,0)和B(-a,0)旋转,且它们在y轴上的截距的乘积bb1=a2(常数),试求旋转杆交点的轨迹方程.
如图,二杆各绕点A(a,0)和B(-a,0)旋转,且它们在y轴上的截距的乘积bb1=a2(常数),试求旋转杆交点的轨迹方程. 如图圆O是半径为1的圆,点PO、P1、P2…、P11将圆12等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3,…,11)的取值集合是{-1,-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,0,$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,1}.
如图圆O是半径为1的圆,点PO、P1、P2…、P11将圆12等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3,…,11)的取值集合是{-1,-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,0,$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,1}. 已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为π.
已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为π.