题目内容

9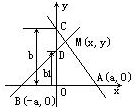．如图，二杆各绕点A（a，0）和B（-a，0）旋转，且它们在y轴上的截距的乘积bb1=a2（常数），试求旋转杆交点的轨迹方程．

分析 求出直线方程，相乘，利用条件，即可求旋转杆交点的轨迹方程．

解答 解：设M（x，y）是两杆交点，则y=-$\frac{b}{a}$（x-a）（1）；y=$\frac{{b}_{1}}{a}$（x+a）（2）
相乘，得y2=-$\frac{b{b}_{1}}{{a}^{2}}$（x2-a2）
将bb1=a2代入上式并整理，得x2+y2=a2 
由bb1=a2（常数），得b、b1不为0，因而y≠0，x≠±a．
故所求轨迹方程为x2+y2=a2（-a＜x＜a）

点评 本题考查轨迹方程，考查直接法的运用，考查学生的计算能力，属于中档题．

练习册系列答案
相关题目
4．$\sqrt{{9}^{\frac{3}{2}}}$的值为（　　）
A．$\sqrt{3}$B．3$\sqrt{3}$C．3D．729
20．已知f（x+y）=f（x）+f（y），判断其奇偶性．
17．已知函数y=f（x）（x∈R）满足f（1+x）=f（x-1），且当x∈（-1，1]时，f（x）=|x|；y=g（x）是定义在R上的奇函数，当x＞0时，g（x）=log3x，则有方程f（x）=g（x）的根的个数为（　　）
A．1B．2C．3D．4
4．在平面直角坐标系中，过动点P分别作圆C1：x2+y2-4x-6y+9=0与圆C2：x2+y2+2x+2y+1=0的切线PA与PB（A，B为切点），若|PA|=|PB|若O为原点，则|OP|的最小值为（　　）
A．2B．$\frac{4}{5}$C．$\frac{3}{5}$D．$\sqrt{5}$
14．（$\sqrt{x}$+$\frac{1}{x}$）n的展开式中只有第六项的二项式系数最大，则第四项为120$\sqrt{x}$．
1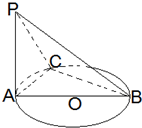．如图，AB是圆O的直径，PA⊥圆O所在的平面，C是圆周上不同于A、B的任意一点，则图中互相垂直的平面共有（　　）
A．2对B．3对C．4对D．5对
18．已知△ABC的两个顶点A，B的坐标分别是（0，-1），（0，1），且AC，BC所在直线的斜率之积等于m（m≠0）．
（1）求顶点C的轨迹E的方程，并判断轨迹E为何种圆锥曲线；
（2）当m=-$\frac{1}{2}$时，直线l不过原点O且不平行于坐标轴，l与E有两个交点A，B，线段AB的中点为M，试问：直线OM的斜率与直线l的斜率的乘积是否为定值．若是，求出定值，若不是，请说明理由．
19．已知函数f（x）=（$\frac{1}{2}$）x，a、b∈R+，A=f（$\frac{a+b}{2}$），B=f（$\sqrt{ab}$），C=f（$\frac{ab}{a+b}$），则A、B、C的大小关系是（　　）
A．A≤B≤CB．A≤C≤BC．B≤C≤AD．C≤B≤A

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网