题目内容
11. 已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为π.
已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为π.(Ⅰ)求f($\frac{3π}{4}$);
(Ⅱ)在给定的平面直角坐标系中,画出函数y=f(x)在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象.
分析 (1)根据T=$\frac{2π}{ω}$,求出周期,得到函数的解析式,代入值计算即可;
(2)利用五点作图法作图即可.
解答 解:(1)依题意得,T=$\frac{2π}{ω}$=π,解得ω=2,所以f(x)=sin(2x-$\frac{π}{4}$),
所以 f($\frac{3}{4}$π)=sin(2×$\frac{3π}{4}$-$\frac{π}{4}$)=sin(π+$\frac{π}{4}$)=-sin$\frac{π}{4}$=-$\frac{\sqrt{2}}{2}$,
(2)画出函数在区间上的图象如图所示: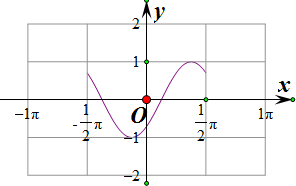
点评 本题考查了三角函数的周期性质,以及三角函数值的求法和函数图象的做法,属于基础题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
1.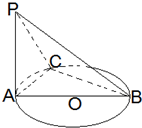 如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中互相垂直的平面共有( )
如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中互相垂直的平面共有( )
 如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中互相垂直的平面共有( )
如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中互相垂直的平面共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
19.已知函数f(x)=($\frac{1}{2}$)x,a、b∈R+,A=f($\frac{a+b}{2}$),B=f($\sqrt{ab}$),C=f($\frac{ab}{a+b}$),则A、B、C的大小关系是( )
| A. | A≤B≤C | B. | A≤C≤B | C. | B≤C≤A | D. | C≤B≤A |
6.某班有50名学生,某次数学成绩经计算后得到的平均数是65分,标准差是s,后来发现记录有误,甲得65分却记为56分,乙得45分误记为54分,更正后重新计算,标准差为s1,则s与s1之间的大小关系是( )
| A. | s═s1 | B. | s>s1 | C. | s<s1 | D. | 不能确定 |
16.计算:$\int_1^2{{{(x-1)}^5}dx}$=( )
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $-\frac{1}{6}$ | D. | $\frac{1}{6}$ |
3.下列函数中,在(0,+∞)上为增函数的是( )
| A. | y=$\sqrt{x+1}$ | B. | y=(x-2)2 | C. | y=3-x | D. | y=log0.1(x+1) |
20.双曲线$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{3}$=1的离心率为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{3\sqrt{2}}{2}$ |