题目内容
1．
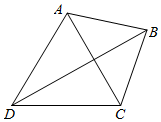某学习小组进行课外研究性学习，为了测量如图所示不能到达的A、B两地，他们测得C、D两地的直线距离为2km，并用仪器测得相关角度大小分别为∠ADB=30°，∠CDB=30°，∠ACD=60°，∠ACB=45°，则A、B两地的距离大约等于（ ）（提供数据：$\sqrt{2}≈1.414，\sqrt{3}≈1.732$，结果保留两个有效数字）| A． | 1.3 | B． | 1.4 | C． | 1.5 | D． | 1.6 |
分析 在△ADC中，可求得AC=2，在△BDC中，利用正弦定理可求得BC，最后在△ABC中，利用余弦定理可求得AB．
解答 解：依题意，△ADC为等边三角形，
∴AC=2．
在△BDC中，CD=2，由正弦定理得：$\frac{BC}{sin30°}=\frac{CD}{sin45°}$=2$\sqrt{2}$，
∴BC=$\sqrt{2}$．
在△ABC中，由余弦定理得AB2=BC2+AC2-2BC•ACcos45°=2+4-2×$\sqrt{2}$×2×$\frac{\sqrt{2}}{2}$=2，
∴AB=$\sqrt{2}$≈1.4km．
故选：B．
点评 本题考查正弦定理与余弦定理，考查解三角形，考查分析与运算能力，属于中档题．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
如图，在四棱锥O-ABCD中，底面ABCD是边长为2的正方形，侧棱OB⊥底面ABCD，且侧棱OB的长是2，点E，F，G分别是AB，OD，BC的中点．
12．设全集U=R，已知集合A={-2，-1，0，1，2，3}，B={x|$\frac{3}{x-1}$+1≥0}，则集合A∩∁UB=（ ）
| A． | {-1，0，1} | B． | {-1，0} | C． | {-2，-1，0，1} | D． | {-1，0，1，2} |
9．某火锅店为了了解气温对营业额的影响，随机记录了该店1月份中5天的日营业额y（单位：千元）与该地当日最低气温x（单位：℃）的数据，如表：
（Ⅰ）求y关于x的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$
（Ⅱ）判定y与x之间是正相关还是负相关；若该地1月份某天的最低气温为6℃，用所求回归方程预测该店当日的营业额
附：回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$．
| x | 2 | 5 | 8 | 9 | 11 |
| y | 12 | 10 | 8 | 8 | 7 |
（Ⅱ）判定y与x之间是正相关还是负相关；若该地1月份某天的最低气温为6℃，用所求回归方程预测该店当日的营业额
附：回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$．
16．若cos（${\frac{π}{6}$-α）=$\frac{1}{3}$，则cos（$\frac{2π}{3}$+2α）=（ ）
| A． | $\frac{2}{9}$ | B． | $-\frac{2}{9}$ | C． | $\frac{7}{9}$ | D． | $-\frac{7}{9}$ |
10．下列命题中，真命题是（ ）
| A． | “a≤b”是“a+c≤b+c”的必要不充分条件 | |
| B． | 如果空间两条直线不相交，则这两条直线平行 | |
| C． | 设命题p：?x∈R，x2+1＞0，则￢p为?x0∈R，x02+1＜0 | |
| D． | “若α=$\frac{π}{4}$，则tanα=1”的逆否命题为“若tanα≠1，则α≠$\frac{π}{4}$” |