题目内容
在平面直角坐标系上,设不等式组
(n∈N*)表示的平面区域为Dn,记Dn内的整点(横坐标和纵坐标均为整数的点)的个数为an.
(1)求出a1,a2,a3的值(不要求写过程);
(2)求数列{an}的通项公式;
(3)令bn=
(n∈N*),求b1+b2+…+bn.
|
(1)求出a1,a2,a3的值(不要求写过程);
(2)求数列{an}的通项公式;
(3)令bn=
| 1 |
| anan+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)画出可行域,结合图形写出a1,a2,a3的值.
(2)根据题设条件,确定x,y的取值范围,结合图形分情况讨论,能求出数列{an}的通项公式.
(3)利用数列{an}的通项公式,求出bn,再利用裂项求和法能求出b1+b2+…+bn.
(2)根据题设条件,确定x,y的取值范围,结合图形分情况讨论,能求出数列{an}的通项公式.
(3)利用数列{an}的通项公式,求出bn,再利用裂项求和法能求出b1+b2+…+bn.
解答:
解:(1)a1=4+2+1=7,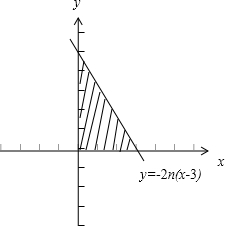
a2=8+4+1=13,
a3=12+6+1=19.
(2)∵y≥0,
∴y=-2n(x-3)≥0,
∴0<x≤3
又∵x是整数
∴x=1,2,3
当x=1有4n个点,当x=2有2n个点,当x=3时,有1个点,
∴an=4n+2n+1=6n+1.
(3)∵an=6n+1,
∴bn=
=
=
(
-
),
∴b1+b2+…+bn
=
(
-
+
-
+
-
+…+
-
)
=
(
-
).

a2=8+4+1=13,
a3=12+6+1=19.
(2)∵y≥0,
∴y=-2n(x-3)≥0,
∴0<x≤3
又∵x是整数
∴x=1,2,3
当x=1有4n个点,当x=2有2n个点,当x=3时,有1个点,
∴an=4n+2n+1=6n+1.
(3)∵an=6n+1,
∴bn=
| 1 |
| anan+1 |
| 1 |
| (6n+1)(6n+7) |
| 1 |
| 6 |
| 1 |
| 6n+1 |
| 1 |
| 6n+7 |
∴b1+b2+…+bn
=
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 13 |
| 1 |
| 13 |
| 1 |
| 19 |
| 1 |
| 19 |
| 1 |
| 25 |
| 1 |
| 6n+1 |
| 1 |
| 6n+7 |
=
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 6n+7 |
点评:本题考查画不等式组表示的平面区域;数列求和的方法:错位相减法、公式法、裂项相消法,是中档题.

练习册系列答案
相关题目
已知自由落体运动的速率v=gt,则落体运动从t=0到t=t0所走的路程为( )
A、
| ||
| B、gt02 | ||
C、
| ||
D、
|
 某几何体的三视图如图所示,则该几何体的表面积是( )
某几何体的三视图如图所示,则该几何体的表面积是( )A、(2+
| ||
B、(4+
| ||
| C、4π | ||
| D、6π |
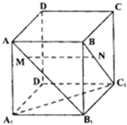 如图,正方体ABCD-A1B1C1D1棱长为1,点M∈AB1,N∈BC1,且AM=BN≠
如图,正方体ABCD-A1B1C1D1棱长为1,点M∈AB1,N∈BC1,且AM=BN≠ 已知函数
已知函数