题目内容
10.化简:${C}_{m}^{7}$-C${\;}_{m+1}^{8}$+C${\;}_{m}^{8}$.分析 直接利用组合数的运算法则化简求解即可.
解答 解:${C}_{m}^{7}$-C${\;}_{m+1}^{8}$+C${\;}_{m}^{8}$=$\frac{m!}{7!•(m-7)!}$-$\frac{(m+1)m!}{8!•(m-7)!}$+$\frac{m!}{8!•(m-8)!}$=$\frac{8•m!-(m+1)m!+(m-7)m!}{8!•(m-7)!}$=0.
点评 本题考查组合数的运算法则的应用,考查计算能力.

练习册系列答案
相关题目
15.已知数列{an}满足a1=-1,|an-an-1|=2n-1(n∈N,n≥2),且{a2n-1}是递减数列,{a2n}是递增数列,则a2016=$\frac{{2}^{2016}-1}{3}$.
2.已知0<a<b<c,且a,b,c是成等比数列的整数,n为大于1的整数,则logan,logbn,logcn( )
| A. | 成等差数列 | B. | 成等比数列 | ||
| C. | 各项倒数成等差数列 | D. | 以上都不对 |
10.如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表.某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
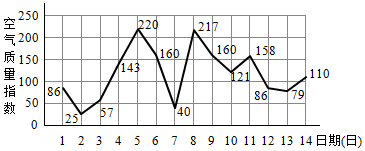
(Ⅰ)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(Ⅱ)求此人到达当日空气质量优良的概率;
(Ⅲ)设X是此人出差期间(两天)空气质量中度或重度重度污染的天数,求X的分布列与数学期望.

(Ⅰ)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(Ⅱ)求此人到达当日空气质量优良的概率;
(Ⅲ)设X是此人出差期间(两天)空气质量中度或重度重度污染的天数,求X的分布列与数学期望.
| 空气质量指数 | 污染程度 |
| 小于100 | 优良 |
| 大于100且小于150 | 轻度 |
| 大于150且小于200 | 中度 |
| 大于200且小于300 | 重度 |
| 大于300且小于500 | 严重 |
| 大于500 | 爆表 |