题目内容
15.在半径为$\sqrt{2}$的⊙O中,直线l和⊙O相切于点C,将直线l匀速向上移动,弧$\widehat{ACB}$所对的圆心角为x,直线l扫过的面积为y=f(x),则y=f(x)的图象大致是( )| A. |  | B. | 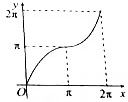 | C. | 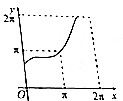 | D. | 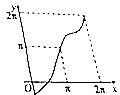 |
分析 求出函数的解析式,分析其单调性,即可得出结论.
解答 解:由题意,x=0时,f(x)=0;x=π时,f(x)=2π,排除C,D;
0<x<π时,f(x)=$\frac{1}{2}×\sqrt{2}x×\sqrt{2}$-$\frac{1}{2}×\sqrt{2}×\sqrt{2}×sinx$=x-sinx,
∴f′(x)=1-cosx,∴f″(x)=sinx>0,
∴0<x<π时,函数单调递增,且增长速度越来越快,
故选:A.
点评 本题考查函数的图象,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.设函数f1(x)=x2,f2(x)=$\frac{3}{x+1}$,f3(x)=sinπx,xi=$\frac{i}{9}$(i=0,1,2,…,9),记Ik=$\sum_{i=1}^{9}$|fk(xi)-fk(xi-1)|,则( )
| A. | I1<I2<I3 | B. | I2<I1<I3 | C. | I3<I2<I1 | D. | I1<I3<I2 |
15.已知双曲线C:${x^2}-\frac{y^2}{8}=1$的左右焦点分别是F1,F2,过F2的直线l与C的左右两支分别交于A,B两点,且|AF1|=|BF1|,则|AB|=( )
| A. | $2\sqrt{2}$ | B. | 3 | C. | 4 | D. | $2\sqrt{2}+1$ |
 将3种作物全部种植在如图的5块试验田里,每块试验田种植一种作物且相邻的试验田不能种植同一种作物,则共有多少种种植方法?
将3种作物全部种植在如图的5块试验田里,每块试验田种植一种作物且相邻的试验田不能种植同一种作物,则共有多少种种植方法?