题目内容
8.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=2,且|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
分析 求出$\overrightarrow{a}•\overrightarrow{b}$,代入向量的夹角公式即可.
解答 解:∵$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}-\overrightarrow{a}•\overrightarrow{b}=2$.∴$\overrightarrow{a}•\overrightarrow{b}$=${\overrightarrow{a}}^{2}-2$=-1.
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=-\frac{1}{2}$.
∴<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{2π}{3}$.
故选D.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
相关题目
19.执行如图所示的程序框图,输出P的值为( )


| A. | -1 | B. | 1 | C. | 0 | D. | 2016 |
17.已知点F1,F2分别是双曲线x2-$\frac{{y}^{2}}{24}$=1的左右焦点,P为该双曲线上一点,且|PF1|=$\frac{4}{3}$|PF2|,则△F1PF2的面积为( )
| A. | $\frac{24}{49}$ | B. | 12 | C. | $\frac{12}{49}$ | D. | 24 |
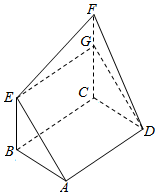 如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF且BE<CF,∠BCF=$\frac{π}{2}$,AD=$\sqrt{3}$,EF=2.
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF且BE<CF,∠BCF=$\frac{π}{2}$,AD=$\sqrt{3}$,EF=2.