题目内容
16.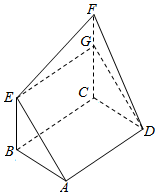 如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF且BE<CF,∠BCF=$\frac{π}{2}$,AD=$\sqrt{3}$,EF=2.
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF且BE<CF,∠BCF=$\frac{π}{2}$,AD=$\sqrt{3}$,EF=2.(1)求证:AE∥平面DCF;
(2)若$BE=\sqrt{3}-1$,且$\frac{AB}{BE}$=λ,当λ取何值时,直线AE与BF所成角的大小为600?
分析 (1)推导出面ABE∥面CDF,由此能证明AE∥面CDF.
(2)以C为坐标原点,以CB,CD,CF分别为x,y,z轴建系,利用向量法能求出当λ取1时,直线AE与BF所成角的大小为60°.
解答  证明:(1)∵BE∥CF,AB∥CD,且BE∩AB=B,FC∩CD=C,
证明:(1)∵BE∥CF,AB∥CD,且BE∩AB=B,FC∩CD=C,
∴面ABE∥面CDF,
又AE?面ABE,∴AE∥面CDF.
解:(2)∵∠BCF=$\frac{π}{2}$,且面ABCD⊥面BEFC,∴FC⊥面ABCD
以C为坐标原点,以CB,CD,CF分别为x,y,z轴建系,
∵$BE=\sqrt{3}-1$,且$\frac{AB}{BE}$=λ,∴AB=($\sqrt{3}-1$)λ,
∴A($\sqrt{3}$,($\sqrt{3}-1$)λ,0),E($\sqrt{3}$,0,$\sqrt{3}-1$),F(0,0,$\sqrt{3}$),B($\sqrt{3}$,0,0),
$\overrightarrow{AE}$=(0,(1-$\sqrt{3}$)λ,$\sqrt{3}-1$),$\overrightarrow{BF}$=(-$\sqrt{3}$,0,$\sqrt{3}$),
∵直线AE与BF所成角的大小为60°,
∴cos60°=$\frac{|\overrightarrow{AE}•\overrightarrow{BF}|}{|\overrightarrow{AE}|•|\overrightarrow{BF}|}$=$\frac{3-\sqrt{3}}{\sqrt{6}•\sqrt{(\sqrt{3}-1)^{2}+(1-\sqrt{3})^{2}{λ}^{2}}}$,
由λ>0,解得λ=1,
∴当λ取1时,直线AE与BF所成角的大小为60°.
点评 本题考查线面平行的证明,考查线段比值使线线角为60°的确定,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | $\frac{{5\sqrt{3}}}{2}$ | B. | $\frac{5}{2}$ | C. | $5\sqrt{3}$ | D. | 5 |
 2016年2月,为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.5,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )
2016年2月,为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.5,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )| A. | 9 | B. | $\frac{9}{2}$ | C. | 8 | D. | 4 |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |