题目内容
已知函数f(x)=x2014+ax2-
-8,f(-2)=10,则f(2)= .
| b |
| x2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由已知函数解析式及f(-2)可求22014+4a-
,然后代入即可求解f(2)
| b |
| 4 |
解答:
解:∵f(x)=x2014+ax2-
-8,
∴f(-2)=(-2)2014+a(-2)2-
-8=10
∴22014+4a-
=18
则f(2)=22014+4a-
-8=10
故答案为:10
| b |
| x2 |
∴f(-2)=(-2)2014+a(-2)2-
| b |
| (-2)2 |
∴22014+4a-
| b |
| 4 |
则f(2)=22014+4a-
| b |
| 4 |
故答案为:10
点评:本题主要考查了函数的性质的简单应用,解题的关键是整体思想的应用.

练习册系列答案
相关题目
曲线y=sinx,x∈[0,2π]与坐标轴围成的面积( )
| A、4 | B、3 | C、2 | D、0 |
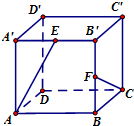 正方体ABCD-A′B′C′D′中,点E为A1B1的中点,F为B1B的中点,则AE与CF所成角的余弦值为
正方体ABCD-A′B′C′D′中,点E为A1B1的中点,F为B1B的中点,则AE与CF所成角的余弦值为