题目内容
一轮船行驶时,单位时间的燃料费u与其速度v的立方成正比,若轮船的速度为每小时10km 时,燃料费为每小时35元,其余费用每小时为560元,这部分费用不随速度而变化.已知该轮船最高速度为25km/h,则轮船速度为 km/h时,轮船航行每千米的费用最少.
考点:余弦定理
专题:解三角形
分析:由题意可得u=kv3(k≠0),由已知求得 k=
,可得u=
v3.根据轮船行驶1千米的费用y=u•
+560•
利用基本不等式求得y的最小值,可得结论.
| 7 |
| 200 |
| 7 |
| 200 |
| 1 |
| v |
| 1 |
| v |
解答:
解:设轮船的燃料费u与速度v之间的关系是:u=kv3(k≠0),
由已知,当v=10时,u=35,∴35=k×103,∴k=
,u=
v3.
∴轮船行驶1千米的费用y=u•
+560•
=
•v2+
+
≥3
=42(元);
当且仅当
=
,即v=20(km/h)时,等号成立.
答:当轮船速度为20km/h时,轮船行每千米的费用最少,最少费用为42元.
由已知,当v=10时,u=35,∴35=k×103,∴k=
| 7 |
| 200 |
| 7 |
| 200 |
∴轮船行驶1千米的费用y=u•
| 1 |
| v |
| 1 |
| v |
| 7 |
| 200 |
| 280 |
| v |
| 280 |
| v |
| 3 |
| ||||||
当且仅当
| 7v2 |
| 200 |
| 280 |
| v |
答:当轮船速度为20km/h时,轮船行每千米的费用最少,最少费用为42元.
点评:本题考查了正比例函数、均值不等式的应用,熟练掌握是解题的关键,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
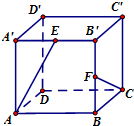 正方体ABCD-A′B′C′D′中,点E为A1B1的中点,F为B1B的中点,则AE与CF所成角的余弦值为
正方体ABCD-A′B′C′D′中,点E为A1B1的中点,F为B1B的中点,则AE与CF所成角的余弦值为