��Ŀ����
1��ѧϰ���к���y=tanx����ѧ�硱���ķ�ͬѧ���Լ��ġ���ѧ���䡱�У�������������ϵͳ�����������к��������ں�������С�������ǦУ������к������溯�����ۺ�����ֵ����ʵ����R���ڶ������������ֵ����Сֵ�������к��������ڵ����ݼ����䣻�����������߲��ཻ��ֱ����x=$\frac{��}{2}$+k�У�k��Z�����������������ĶԳ�ͼ�Σ���Գ����������ǣ�$\frac{k��}{2}$��0����k��Z�������۶�����ȷ���У�������| A�� | 3�� | B�� | 4�� | C�� | 5�� | D�� | 6�� |
���� �������к�����ͼ�����ν�Ͻ����ж�����������
��� 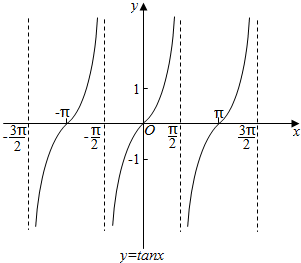 �⣺�������к�����ͼ������ͼ��
�⣺�������к�����ͼ������ͼ��
�������к�����ͼ��õ������к��������ں�������С�������ǦУ��ʢ���ȷ��
�������к�����ͼ�����ԭ��Գƣ��õ����к������溯�����ʢ���ȷ��
�����к�����ֵ����ʵ����R���ڶ������������ֵ����Сֵ���ʢ���ȷ��
�����к����ڣ�k$��-\frac{��}{2}$��$k��+\frac{��}{2}$����k��Z�����������������ڵ����ݼ����䣬�ʢ���ȷ��
��x=$\frac{��}{2}$+k�У�k��Z���������߲��ཻ���ʢ���ȷ��
���������������ĶԳ�ͼ�Σ���Գ����������ǣ�$\frac{k��}{2}$��0����k��Z���ʢ���ȷ��
��ѡ��D��
���� ���⿼��������ٵ��жϣ��ǻ����⣬����ʱҪ�������⣬ע�����к�����ͼ�����ʵĺ������ã�

��ϰ��ϵ�д�
�����Ŀ
11����֪a��b��R�����н��۳������ǣ�������
| A�� | ��a��b����ac��bc | B�� | ��a��b��c��d����ac��bd | ||
| C�� | ��a��b��0����$\frac{1}{a}$��$\frac{1}{b}$ | D�� | ��a��b����an��bn��n��N*��n��2�� |
16������ʽ4x2+4bx+1��0�Ľ⼯Ϊ∅��������
| A�� | b��1 | B�� | b��-1��b��1 | C�� | -1��b��1 | D�� | b��1��b��-1 |
6����P��5��0����Բx2+y2=24��λ�ù�ϵ�ǣ�������
| A�� | ��Բ�� | B�� | ��Բ�� | C�� | ��Բ�� | D�� | ��ȷ�� |
13��cos35��cos70��-sin35��cos20����ڣ�������
| A�� | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | B�� | -$\frac{\sqrt{6}+\sqrt{2}}{4}$ | C�� | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D�� | $\frac{\sqrt{2}-\sqrt{6}}{4}$ |