题目内容
已知某篮球选手罚球投蓝的命中概率为
,在进行三次罚蓝中命中两次的概率为 (用数字作答).
| 4 |
| 5 |
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:利用n次独立重复试验中事件A恰好发生k次的概率计算公式能求出结果.
解答:
解:∵某篮球选手罚球投蓝的命中概率为
,
∴在进行三次罚蓝中命中两次的概率为:
P=
(
)2(
)=
.
故答案为:
.
| 4 |
| 5 |
∴在进行三次罚蓝中命中两次的概率为:
P=
| C | 2 3 |
| 4 |
| 5 |
| 1 |
| 5 |
| 48 |
| 125 |
故答案为:
| 48 |
| 125 |
点评:本题考查概率的求法,是基础题,解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.

练习册系列答案
相关题目
在平面直角坐标系xOy中,设不等式组
,所表示的平面区域为D,若D的边界是菱形,则ab=( )
|
A、-2
| ||
B、2
| ||
C、2
| ||
D、-2
|
f(x)=2sin(x-
),x∈[0,
]则f(x)的最大值为( )
| π |
| 4 |
| π |
| 2 |
| A、2 | ||
| B、0 | ||
C、
| ||
| D、1 |
如果向量
=(2,1),
=(-3,4),那么向量3
+4
的坐标是( )
| a |
| b |
| a |
| b |
| A、(19,-6) |
| B、(-6,19) |
| C、(-1,16) |
| D、(16,-1) |
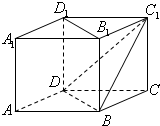
如图所示,在正方体ABCD-A1B1C1D1中,直线B1D1与平面BDC1的位置关系是( )

| A、平行 |
| B、垂直 |
| C、相交但不垂直 |
| D、直线B1D1在平面BDC1内 |
三个数a=30.4,b=0.43,c=log0.43大小关系为( )
| A、b<c<a |
| B、b<a<c |
| C、b<a<c |
| D、c<b<a |