题目内容
2.已知点P,Q的坐标分别为(-1,1),(2,2),若直线l:x+my+m=0与PQ的延长线相交,则实数m的取值范围是-3<m<-$\frac{2}{3}$.分析 先求出PQ的斜率,再分情况讨论出直线的几种特殊情况,综合即可得到答案.
解答 解:由题知kPQ=$\frac{2-1}{2-(-1)}$=$\frac{1}{3}$,
直线x+my+m=0过点M(0,-1).
当m=0时,直线化为x=0,一定与PQ相交,所以m≠0,
当m≠0时,kl=-$\frac{1}{m}$,考虑直线l的两个极限位置.
(1)l经过Q,即直线l1,则${k}_{{l}_{1}}$=$\frac{2-(-1)}{2-0}$=$\frac{3}{2}$;
(2)l与PQ平行,即直线l2,则${k}_{{l}_{2}}$=kPQ=$\frac{1}{3}$,
∴$\frac{1}{3}$<-$\frac{1}{m}$<$\frac{3}{2}$,
∴-3<m<-$\frac{2}{3}$,
故答案为:-3<m<-$\frac{2}{3}$.
点评 本题主要是考查直线之间的位置关系.其中涉及到分类讨论思想的应用,属于基础题目.

练习册系列答案
相关题目
14.已知变量x,y满足线性约束条件$\left\{\begin{array}{l}{x+y+1≥0}\\{x-y+2≥0}\\{3x+y-2≤0}\end{array}\right.$,若目标函数z=ax-y仅在点(0,2)处取得最小值,则实数a的取值范围是( )
| A. | (-∞,-3) | B. | (3,+∞) | C. | (-3,1) | D. | (-1,1) |
11.已知集合A={y|y=$\sqrt{{x}^{2}-1}$},B={x|x2-1<0},则A∩B=( )
| A. | ∅ | B. | {x|0≤x<1} | C. | {x|x≥0} | D. | {x|0<x<1} |
17.执行如图的程序框图,若输入的a,b,k分别为1,2,4,则输出的M=( )


| A. | $\frac{8}{3}$ | B. | $\frac{15}{8}$ | C. | $\frac{16}{5}$ | D. | $\frac{20}{3}$ |
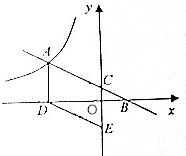 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.