题目内容
15．对于100个黑球和99个白球的任意排列（从左到右排成一行），则一定（ ）| A． | 存在一个白球，它右侧的白球和黑球一样多 | |
| B． | 存在一个黑球，它右侧的白球和黑球一样多 | |
| C． | 存在一个白球，它右侧的白球比黑球少一个 | |
| D． | 存在一个黑球，它右侧的白球比黑球少一个 |
分析 100个黑球和99个白球，99为奇数，100为偶数，分析即可得到答案．
解答 解：99为奇数，100为偶数，故总存在一个黑球，它右侧的白球和黑球一样多，
故选：B．
点评 本题考查了合情推理的问题，关键是读清题意，属于基础题．
练习册系列答案
相关题目
8．设f'（x）是函数f（x）（x∈R）的导数，且满足xf'（x）-2f（x）＞0，若△ABC中，∠C是钝角，则（ ）
| A． | f（sinA）•sin2B＞f（sinB）•sin2A | B． | f（sinA）•sin2B＜f（sinB）•sin2A | ||
| C． | f（cosA）•sin2B＞f（sinB）•cos2A | D． | f（cosA）•sin2B＜f（sinB）•cos2A |
6．在△ABC中，D为三角形所在平面内一点，且$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$，则$\frac{{{S_{△BCD}}}}{{{S_{△ABD}}}}$=（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
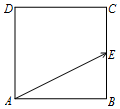
B．
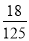
D．