题目内容
6.在△ABC中,D为三角形所在平面内一点,且$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$,则$\frac{{{S_{△BCD}}}}{{{S_{△ABD}}}}$=( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 利用三角形以及向量关系,求解三角形的面积即可.
解答  解:由已知,在△ABC中,D为三角形所在平面内一点,
解:由已知,在△ABC中,D为三角形所在平面内一点,
且$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$,
点D在平行于AB的中位线上,且为靠近AC边,
从而有${S_{△ABD}}=\frac{1}{2}{S_{△ABC}}$,${S_{△ACD}}=\frac{1}{3}{S_{△ABC}}$,
${S_{△BCD}}=(1-\frac{1}{2}-\frac{1}{3}){S_{△ABC}}=\frac{1}{6}{S_{△ABC}}$,有$\frac{{{S_{△BCD}}}}{{{S_{△ABD}}}}=\frac{1}{3}$.
故选:B.
点评 本题主要考查利用平面向量确定点的位置进而解决平几问题.

练习册系列答案
相关题目
15.对于100个黑球和99个白球的任意排列(从左到右排成一行),则一定( )
| A. | 存在一个白球,它右侧的白球和黑球一样多 | |
| B. | 存在一个黑球,它右侧的白球和黑球一样多 | |
| C. | 存在一个白球,它右侧的白球比黑球少一个 | |
| D. | 存在一个黑球,它右侧的白球比黑球少一个 |
1.已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如表:
若抽取学生n人,成绩分为A(优秀),B(良好),C(及格)三个等次,设x,y分别表示数学成绩与地理成绩,例如:表中地理成绩为A等级的共有14+40+10=64(人),数学成绩为B等级且地理成绩为C等级的有8人.已知x与y均为A等级的概率是0.07.
(1)设在该样本中,数学成绩的优秀率是30%,求a,b的值;
(2)已知a≥8,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
| x 人数 y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
(1)设在该样本中,数学成绩的优秀率是30%,求a,b的值;
(2)已知a≥8,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
18.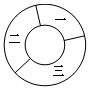 某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )
某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )
 某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )
某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{7}$ | D. | $\frac{3}{8}$ |
14.已知正三角形ABC的顶点A,B在抛物线y2=4x上,另一个顶点C(4,0),则这样的正三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |

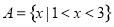 ,集合
,集合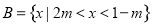 .
.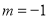 时,求
时,求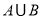 ;
;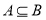 ,求实数
,求实数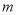 的取值范围;
的取值范围;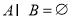 ,求实数
,求实数 的取值范围.
的取值范围.