题目内容
19.我国古代数学名著《张邱健算经》有“分钱问题”如下:“今有人与钱,初一人与三钱,次一人与四钱,次一人与五钱,以次与之,转多一钱,与讫,还数聚与均分之,人得一百钱,问人几何?”则分钱问题中的人数为195.分析 由题意,意思是:将钱分给若干人,第一人给3钱,第二人给4钱,第三人给5钱,以此类推,每人比前一人多给1钱,分完后,再把钱收回平均分给各人,结果每人分得100钱,问有多少人?是一个等差数列的问题.设人数为n,公差为1,首项为3.求前n项和等于100n,可得答案.
解答 解:设人数为n,公差为1,首项为3.
则前n项和${S}_{n}=\frac{n(n-1)}{2}+3n$.
由题意:Sn=100n,即$\frac{n(n-1)}{2}+3n=100n$,
解得:n=195.
故答案为195
点评 本题考查了对文字意思的理解和关系式的建立.属于基础题.

练习册系列答案
相关题目
13.已知集合A={-2,-1,1,2},B={x|lgx≤1},则A∩B=( )
| A. | {-2,-1,1,2} | B. | {-2,-1,1} | C. | {1} | D. | {1,2} |
8.已知函数$f(x)=\left\{{\begin{array}{l}{1-|x-1|(x≤2)}\\{{e^{x-2}}(-{x^2}+8x-12)(x>2)}\end{array}}\right.$,如在区间(1,+∞)上存在n(n≥2)个不同的数x1,x2,x3,…,xn,使得比值$\frac{f({x}_{1})}{{x}_{1}}$=$\frac{f({x}_{2})}{{x}_{2}}$=…=$\frac{f({x}_{n})}{{x}_{n}}$成立,则n的取值集合是( )
| A. | {2,3,4,5} | B. | {2,3} | C. | {2,3,5} | D. | {2,3,4} |
15.对于100个黑球和99个白球的任意排列(从左到右排成一行),则一定( )
| A. | 存在一个白球,它右侧的白球和黑球一样多 | |
| B. | 存在一个黑球,它右侧的白球和黑球一样多 | |
| C. | 存在一个白球,它右侧的白球比黑球少一个 | |
| D. | 存在一个黑球,它右侧的白球比黑球少一个 |
4.圆(x-2)2+y2=4关于直线$y=\frac{{\sqrt{3}}}{3}x$对称的圆的方程是( )
| A. | ${(x-\sqrt{3})^2}+{(y-1)^2}=4$ | B. | ${(x-\sqrt{2})^2}+{(y-\sqrt{2})^2}=4$ | C. | x2+(y-2)2=4 | D. | ${(x-1)^2}+{(y-\sqrt{3})^2}=4$ |
8.设i为虚数单位,则复数z=$\frac{1+2i}{i}$的虚部为( )
| A. | -2 | B. | -i | C. | i | D. | -1 |

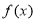 是定义在
是定义在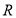 上的偶函数,且在区间
上的偶函数,且在区间 上单调递增,若实数
上单调递增,若实数 满足
满足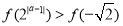 ,则
,则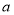 的取值范围是( )
的取值范围是( )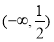 B.
B.
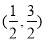 D.
D.