题目内容
10.已知{an}为等差数列,公差为d,且0<d<1,a5≠$\frac{kπ}{2}$(k∈Z),sin2a3+2sina5•cosa5=sin2a7,函数f(x)=dsin(wx+4d)(w>0)满足:在$x∈(0,\frac{3π}{4})$上单调且存在${x_0}∈(0,\frac{3π}{4}),f(x)+f(2{x_0}-x)=0$,则w范围是0<w≤$\frac{4}{3}$..分析 推导出sin4d=1,由此能求出d,可得函数解析式,利用在$x∈(0,\frac{3π}{4})$上单调且存在${x_0}∈(0,\frac{3π}{4}),f(x)+f(2{x_0}-x)=0$,即可得出结论.
解答 解:∵{an}为等差数列,公差为d,且0<d<1,a5≠$\frac{kπ}{2}$(k∈Z),
sin2a3+2sina5•cosa5=sin2a7,
∴2sina5cosa5=sin2a7-sin2a3=2sin$\frac{{a}_{3}+{a}_{7}}{2}$cos$\frac{{a}_{7}-{a}_{3}}{2}$•2cos$\frac{{a}_{3}+{a}_{7}}{2}$sin$\frac{{a}_{7}-{a}_{3}}{2}$=2sina5cos2d•2cosa5sin2d,
∴sin4d=1,
∴d=$\frac{π}{8}$.
∴f(x)=$\frac{π}{8}$coswx,
∵在$x∈(0,\frac{3π}{4})$上单调且存在${x_0}∈(0,\frac{3π}{4}),f(x)+f(2{x_0}-x)=0$,
∴$\frac{π}{w}≥\frac{3π}{4}$,
∴0<w≤$\frac{4}{3}$.
故答案为0<w≤$\frac{4}{3}$.
点评 本题考查等差数列的公差的求法,考查三角函数的图象与性质,是中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
2.若点P是△ABC的外心,且$\overrightarrow{PA}$+$\overrightarrow{PB}$+λ$\overrightarrow{PC}$=$\overrightarrow{0}$,∠C=120°,则实数λ的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | 1 |
15.对于100个黑球和99个白球的任意排列(从左到右排成一行),则一定( )
| A. | 存在一个白球,它右侧的白球和黑球一样多 | |
| B. | 存在一个黑球,它右侧的白球和黑球一样多 | |
| C. | 存在一个白球,它右侧的白球比黑球少一个 | |
| D. | 存在一个黑球,它右侧的白球比黑球少一个 |
1.已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如表:
若抽取学生n人,成绩分为A(优秀),B(良好),C(及格)三个等次,设x,y分别表示数学成绩与地理成绩,例如:表中地理成绩为A等级的共有14+40+10=64(人),数学成绩为B等级且地理成绩为C等级的有8人.已知x与y均为A等级的概率是0.07.
(1)设在该样本中,数学成绩的优秀率是30%,求a,b的值;
(2)已知a≥8,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
| x 人数 y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
(1)设在该样本中,数学成绩的优秀率是30%,求a,b的值;
(2)已知a≥8,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
18.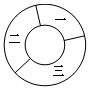 某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )
某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )
 某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )
某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{7}$ | D. | $\frac{3}{8}$ |
18.已知角α终边上一点的坐标为P(sin$\frac{π}{10}$,cos$\frac{9π}{10}$),则角α是( )
| A. | $\frac{π}{10}$ | B. | $\frac{2π}{5}$ | C. | -$\frac{π}{10}$ | D. | -$\frac{2π}{5}$ |
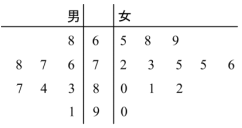 某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示,成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.
某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示,成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”. 且
且 ,则当
,则当 时,
时, 的导函数
的导函数 的极小值为 .
的极小值为 .