题目内容
8.设f'(x)是函数f(x)(x∈R)的导数,且满足xf'(x)-2f(x)>0,若△ABC中,∠C是钝角,则( )| A. | f(sinA)•sin2B>f(sinB)•sin2A | B. | f(sinA)•sin2B<f(sinB)•sin2A | ||
| C. | f(cosA)•sin2B>f(sinB)•cos2A | D. | f(cosA)•sin2B<f(sinB)•cos2A |
分析 求出函数的导数,得到函数的单调性,从而判断出结论即可.
解答 解:∵${[\frac{f(x)}{{x}^{2}}]}^{′}$=$\frac{xf′(x)-2f(x)}{{x}^{3}}$,
x>0时,${[\frac{f(x)}{{x}^{2}}]}^{′}$>0,
∴$\frac{f(x)}{{x}^{2}}$在(0,+∞)递增,
又∵∠C是钝角,∴cosA>sinB>0,
∴$\frac{f(cosA)}{{cos}^{2}A}$>$\frac{f(sinB)}{{sin}^{2}B}$,
∴f(cosA)sin2B>f(sinB)cos2A,
故选:C.
点评 本题考查了函数的单调性问题,考查导数的应用,是一道中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
19.设全集U=A∪B={1,2,3,4,5},A∩(∁UB)={1,2},则集合B=( )
| A. | {2,4,5} | B. | {3,4,5} | C. | {4,5} | D. | (2,4) |
16.函数$f(x)=\frac{lnx}{x}$,则( )
| A. | x=e为函数f(x)的极大值点 | B. | x=e为函数f(x)的极小值点 | ||
| C. | $x=\frac{1}{e}$为函数f(x)的极大值点 | D. | $x=\frac{1}{e}$为函数f(x)的极小值点 |
13.已知集合A={-2,-1,1,2},B={x|lgx≤1},则A∩B=( )
| A. | {-2,-1,1,2} | B. | {-2,-1,1} | C. | {1} | D. | {1,2} |
15.对于100个黑球和99个白球的任意排列(从左到右排成一行),则一定( )
| A. | 存在一个白球,它右侧的白球和黑球一样多 | |
| B. | 存在一个黑球,它右侧的白球和黑球一样多 | |
| C. | 存在一个白球,它右侧的白球比黑球少一个 | |
| D. | 存在一个黑球,它右侧的白球比黑球少一个 |
14.已知正三角形ABC的顶点A,B在抛物线y2=4x上,另一个顶点C(4,0),则这样的正三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
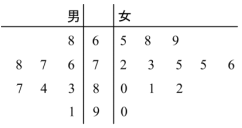 某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示,成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.
某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示,成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.