题目内容
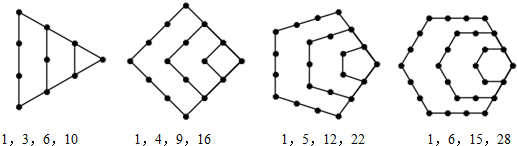
由下面四个图形中的点数分别给出了四个数列的前四项,将每个图形的层数增加可得到这四个数列的后继项.按图中多边形的边数依次称这些数列为“三角形数列”、“四边形数列”…,将构图边数增加到n可得到“n边形数列”,记它的第r项为P(n,r).
(1)求使得P(3,r)>36的最小r的取值;
(2)试推导P(n,r)关于n、r的解析式;
(3)是否存在这样的“n边形数列”,它的任意连续两项的和均为完全平方数.若存在,指出所有满足条件的数列,并证明你的结论;若不存在,请说明理由.

(1)求使得P(3,r)>36的最小r的取值;
(2)试推导P(n,r)关于n、r的解析式;
(3)是否存在这样的“n边形数列”,它的任意连续两项的和均为完全平方数.若存在,指出所有满足条件的数列,并证明你的结论;若不存在,请说明理由.
考点:归纳推理
专题:综合题,推理和证明
分析:(1)由已知可得P(3,r)=
,解不等式可得最小r的取值;
(2)设n边形数列所对应的图形中第r层的点数为a1,则P(n,r)=a1+a2+…+ar,进而由等差数列的前n项和公式,可得答案.
(3)P(n,r+1)+P(n,r)=(n-2)r2+2r+1,n=3时,满足题意;而结论要对于任意的正整数r都成立,则(n-2)r2+2r+1的判别式必须为0,即可得出结论.
| r(r+1) |
| 2 |
(2)设n边形数列所对应的图形中第r层的点数为a1,则P(n,r)=a1+a2+…+ar,进而由等差数列的前n项和公式,可得答案.
(3)P(n,r+1)+P(n,r)=(n-2)r2+2r+1,n=3时,满足题意;而结论要对于任意的正整数r都成立,则(n-2)r2+2r+1的判别式必须为0,即可得出结论.
解答:
解:(1)由题意得:P(3,r)=1+2+…+r=
令
>36
即r2+r-72>0,
解得r>8
∴最小的r=9.
(2)设n边形数列所对应的图形中第r层的点数为a1,
则P(n,r)=a1+a2+…+ar,
从图中可以得出:后一层的点在n-2条边上增加了一点,两条边上的点数不变,
所以ar+1-ar=n-2,a1=1
所以{ar}是首项为1公差为n-2的等差数列,
所以P(n,r)=r+
;
(3)P(n,r+1)+P(n,r)=(n-2)r2+2r+1,
n=3时,满足题意;
而结论要对于任意的正整数r都成立,则(n-2)r2+2r+1的判别式必须为0,
∴4-4(n-2)=0,∴n=3,
故满足题意的数列为“三角形数列”.
| r(r+1) |
| 2 |
令
| r(r+1) |
| 2 |
即r2+r-72>0,
解得r>8
∴最小的r=9.
(2)设n边形数列所对应的图形中第r层的点数为a1,
则P(n,r)=a1+a2+…+ar,
从图中可以得出:后一层的点在n-2条边上增加了一点,两条边上的点数不变,
所以ar+1-ar=n-2,a1=1
所以{ar}是首项为1公差为n-2的等差数列,
所以P(n,r)=r+
| (n-2)r(r-1) |
| 2 |
(3)P(n,r+1)+P(n,r)=(n-2)r2+2r+1,
n=3时,满足题意;
而结论要对于任意的正整数r都成立,则(n-2)r2+2r+1的判别式必须为0,
∴4-4(n-2)=0,∴n=3,
故满足题意的数列为“三角形数列”.
点评:本题考查等差数列的基本知识,递推数列的通项公式的求解等基本方法,考察抽象概括能力以及推理论证能力.

练习册系列答案
相关题目
函数f(x)=x-sin2x的图象为( )
A、 |
B、 |
C、 |
D、 |
点P在双曲线C:
-y2=1上,F1、F2是双曲线的焦点,∠F1PF2=60°,则P到x轴的距离为( )
| x2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|