题目内容
16.已知边长为$2\sqrt{3}$的菱形ABCD中,∠BAD=60°,沿对角线BD折成二面角为120°的四面体,则四面体的外接球的表面积为28π.分析 取BD的中点E,连AE,CE,外接球球心在面ACE内,OG⊥CE,OE垂直平分AC,其中CG=2GE=2,∠CEA=120°,可得四面体的外接球的半径,即可求出四面体的外接球的表面积.
解答  解:如图1,取BD的中点E,连AE,CE.
解:如图1,取BD的中点E,连AE,CE.
由已知条件,面ACE⊥面BCD.则外接球球心在面ACE内,
如图2,OG⊥CE,OE垂直平分AC,其中CG=2GE=2,∠CEA=120°
∴$OG=GE•tan6{0}^{°}=\sqrt{3}$,
得$R=OC=OA=\sqrt{7}$,外接球的表面积为28π.
故答案为:28π.
点评 本题考查四面体的外接球的表面积,考查学生的计算能力,求出四面体的外接球的半径是关键.

练习册系列答案
相关题目
11.已知A(0,1)和直线l:x=-5,抛物线y2=4x上动点P到l的距离为d,则|PA|+d的最小值是( )
| A. | 6 | B. | $5+\sqrt{2}$ | C. | $4+\sqrt{2}$ | D. | $4\sqrt{2}$ |
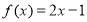 ,
, ,则
,则 的解析式是_______.
的解析式是_______. 在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=4,EF=3,AD=AE=BE=2,G是BC的中点.
在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=4,EF=3,AD=AE=BE=2,G是BC的中点.