题目内容
设a、b、c分别为△ABC三内角A、B、C的对边，若sinB≤2sinCcosA，c=2bcosA，则sin（2A+
）的取值范围是（ ）
| π |
| 3 |
| A、（0，1] | ||
| B、[0，1] | ||
C、（
| ||
D、[0，
|
考点：余弦定理的应用,余弦定理
专题：解三角形
分析：直接利用余弦定理，化简已知条件，推出A的范围，然后求解2A+
的范围，即可推出结果．
| π |
| 3 |
解答：
解：a、b、c分别为△ABC三内角A、B、C的对边，若sinB≤2sinCcosA，
可得：b≤2c×
，可得a≤c．
c=2bcosA=2b×
，可得a=b．
则A∈（0，
]．
2A+
∈（
，π]．
sin（2A+
）∈[0，1]．
故选：B．
可得：b≤2c×
| b2+c2-a2 |
| 2bc |
c=2bcosA=2b×
| b2+c2-a2 |
| 2bc |
则A∈（0，
| π |
| 3 |
2A+
| π |
| 3 |
| π |
| 3 |
sin（2A+
| π |
| 3 |
故选：B．
点评：本题考查余弦定理的应用，三角函数的值域的求法，考查计算能力．
练习册系列答案
53随堂测系列答案
相关题目
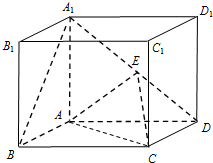如图，在长方体ABCD-A1B1C1D1中，A1A=AD=
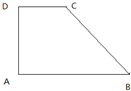在如图所示直角梯形ABCD中，AB∥DC，∠A=90°，AB=AD=2DC=4，画出该梯形的直观图A′B′C′D′，并写出其做法（要求保留作图过程的痕迹．）两圆（x-2）2+（y+3）2=13和（x-3）2+y2=9交于A，B两点，则AB的垂直平分线的方程是（ ）
| A、x+y+3=0 |
| B、2x-y-5=0 |
| C、3x-y-9=0 |
| D、4x-3y+7=0 |