��Ŀ����
��֪�������⣺
����mΪֱ�ߣ�������Ϊƽ�棬��m�ͦ£���m�Φ����ǡ����ͦ¡��ij�Ҫ������
��(x3+
)5��չ��ʽ�к�x3�����ϵ��Ϊ60��
�������������N��0��1������P����2��=p����P��-2����0��=
-p��
��������ʽ|x+3|+|x-2|��2m+1���������m��ȡֵ��Χ�ǣ�-�ޣ�2����
����֪�溯��f��x������f��x+�У�=-f��x������0��x��
ʱf��x��=x������g��x��=f��x��-sinx��[-2�У�2��]����5����㣮
�������������������ǣ�������
����mΪֱ�ߣ�������Ϊƽ�棬��m�ͦ£���m�Φ����ǡ����ͦ¡��ij�Ҫ������
��(x3+
| 1 |
| x |
�������������N��0��1������P����2��=p����P��-2����0��=
| 1 |
| 2 |
��������ʽ|x+3|+|x-2|��2m+1���������m��ȡֵ��Χ�ǣ�-�ޣ�2����
����֪�溯��f��x������f��x+�У�=-f��x������0��x��
| �� |
| 2 |
�������������������ǣ�������
| A���ۢ� | B���� | C���ܢ� | D���ڢ� |
���㣺���������ж���Ӧ��
ר�⣺������
����������mΪֱ�ߣ�������Ϊƽ�棬��m�ͦ£���m�Φ����ǡ����ͦ¡��ij�ֲ���Ҫ������
��(x3+
)5��չ��ʽ��ͨ�ʽTr+1=
(x3)5-r(
)r=
x15-4r����15-4r=3�����r���ɵó���x3�����ϵ����
��������������Ρ�N��0��1����P���Ρ�2��=p���ɵ�P��-2���Σ�0��=
(1-2p)��
�����þ���ֵ����ʽ�����ʲ���ʽ|x+3|+|x-2|��|-3-2|���ɵ�5��2m+1����������m��ȡֵ��Χ��
�����溯��f��x������f��x+�У�=-f��x�����ɵú���f��x��������T=2�У�������f��x������ֱ��x=
�Գƣ�����f��x�����溯������-
��x��
ʱ��f��x��=x����f(
)=1������g��x��=f��x��-sinx��[-2�У�2��]����9����㣮
��(x3+
| 1 |
| x |
| ∁ | r 5 |
| 1 |
| x |
| ∁ | r 5 |
��������������Ρ�N��0��1����P���Ρ�2��=p���ɵ�P��-2���Σ�0��=
| 1 |
| 2 |
�����þ���ֵ����ʽ�����ʲ���ʽ|x+3|+|x-2|��|-3-2|���ɵ�5��2m+1����������m��ȡֵ��Χ��
�����溯��f��x������f��x+�У�=-f��x�����ɵú���f��x��������T=2�У�������f��x������ֱ��x=
| �� |
| 2 |
| �� |
| 2 |
| �� |
| 2 |
| �� |
| 2 |
���
�⣺����mΪֱ�ߣ�������Ϊƽ�棬��m�ͦ£���m�Φ����ǡ����ͦ¡��ij�ֲ���Ҫ��������˲���ȷ��
��(x3+
)5��չ��ʽ��ͨ�ʽTr+1=
(x3)5-r(
)r=
x15-4r����15-4r=3�����r=3��
��x3�����ϵ��Ϊ
=10����˲���ȷ��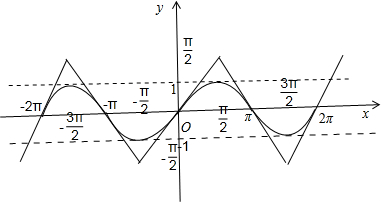
�������������N��0��1������P����2��=p����P��-2����0��=
(1-2p)=
-p��
�����ȷ��
�ܡ߲���ʽ|x+3|+|x-2|��|-3-2|=5����5��2m+1����������m��2����m��ȡֵ��Χ��
��-�ޣ�2]����˲���ȷ��
�ݡ��溯��f��x������f��x+�У�=-f��x������f��x+2�У�=f��x����
f��-x+��=-f��-x��=f��x����
�ຯ��f��x��������T=2�У�f��-x+�У�=f��x����������f��x������ֱ��x=
�Գƣ�
�ߺ���f��x�����溯������0��x��
ʱf��x��=x����-
��x��0��f��x��=x��
�ֱ�����y=f��x����y=sinx��ͼ����f(
)=1������g��x��=f��x��-sinx��[-2�У�2��]����9����㣬��˲���ȷ��
�������������������Ǣۣ�
��ѡ��B��
��(x3+
| 1 |
| x |
| ∁ | r 5 |
| 1 |
| x |
| ∁ | r 5 |
��x3�����ϵ��Ϊ
| ∁ | 3 5 |

�������������N��0��1������P����2��=p����P��-2����0��=
| 1 |
| 2 |
| 1 |
| 2 |
�����ȷ��
�ܡ߲���ʽ|x+3|+|x-2|��|-3-2|=5����5��2m+1����������m��2����m��ȡֵ��Χ��
��-�ޣ�2]����˲���ȷ��
�ݡ��溯��f��x������f��x+�У�=-f��x������f��x+2�У�=f��x����
f��-x+��=-f��-x��=f��x����
�ຯ��f��x��������T=2�У�f��-x+�У�=f��x����������f��x������ֱ��x=
| �� |
| 2 |
�ߺ���f��x�����溯������0��x��
| �� |
| 2 |
| �� |
| 2 |
�ֱ�����y=f��x����y=sinx��ͼ����f(
| �� |
| 2 |
�������������������Ǣۣ�
��ѡ��B��
���������⿼�������洹ֱ���ж�����������ʽ��������̬�ֲ������ʡ�������ֵ�IJ���ʽ�����ʡ���������ż�Ե����ԣ����������ν�ϵ�˼�뷽������������������������������������⣮

��ϰ��ϵ�д�
�����Ŀ
��֪M={x|-1��x��5}��N={x|x��x-4����0}����M��N=��������
| A����-1��0�� |
| B����-1��0���ȣ�4��5�� |
| C����0��4�� |
| D����4��5�� |
��a��b��c�ֱ�Ϊ��ABC���ڽ�A��B��C�ĶԱߣ���sinB��2sinCcosA��c=2bcosA����sin��2A+
����ȡֵ��Χ�ǣ�������
| �� |
| 3 |
| A����0��1] | ||
| B��[0��1] | ||
C����
| ||
D��[0��
|
����A��4��a����B��5��b����ֱ����ֱ��y=x+mƽ�У���|AB|��ֵ�ǣ�������
| A��6 | ||
B��
| ||
| C��2 | ||
| D��1 |
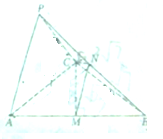 ��ͼ��������P-ABC�У�����ABC�DZ߳�Ϊ4���������Σ�PA=PC=2
��ͼ��������P-ABC�У�����ABC�DZ߳�Ϊ4���������Σ�PA=PC=2